折纸是我国传统的民间艺术,通过折纸不仅可以得到许多美丽的图形,折纸的过程还蕴含着丰富的数学知识,在综合与实践课上,老师让同学们以“正方形的折叠”为主题开展了数学活动.
(1)操作判断:
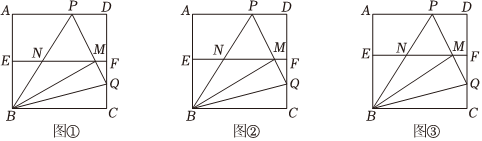
在AD上选一点P,沿BP折叠,使点A落在正方形内部的点M处,把纸片展平,过M作EF∥BC交AB、CD、BP于点E、F、N,连接PM并延长交CD于点Q,连接BQ,如图①,当E为AB中点时,△PMN是 等边等边三角形.∠QBC=15°15°.
(2)迁移探究:
如图②,若BE=5,且ME•MF=10,求正方形ABCD的边长.
(3)拓展应用:
如图③,若MNBC=1n(n>1),直接写出CQBC的值为n-1n+1n-1n+1.
MN
BC
1
n
CQ
BC
n
-
1
n
+
1
n
-
1
n
+
1
【考点】相似形综合题.
【答案】等边;15°;
n
-
1
n
+
1
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/5/15 8:0:8组卷:479引用:1难度:0.5
相似题
-
1.数学课上,王老师出示问题:如图1,将边长为5的正方形纸片ABCD折叠,使顶点A落在边CD上的点P处(点P与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.
(1)观察操作结果,在图1中找到一个与△DEP相似的三角形,并证明你的结论;
(2)当点P在边CD的什么位置时,△DEP与△CPG面积的比是9:25?请写出求解过程;
(3)将正方形换成正三角形,如图2,将边长为5的正三角形纸片ABC折叠,使顶点A落在边BC上的点P处(点P与B、C不重合),折痕为EF,当点P在边BC的什么位置时,△BEP与△CPF面积的比是9:25?请写出求解过程.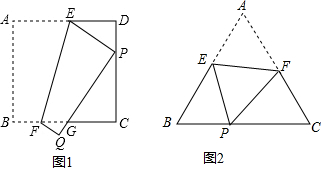 发布:2025/6/15 22:0:1组卷:1072引用:9难度:0.2
发布:2025/6/15 22:0:1组卷:1072引用:9难度:0.2 -
2.在△ABC中,CD是中线,E,F分别为BC,AC上的一点,连接EF交CD于点P.
(1)如图1,若F为AC的中点,CE=2BE,求的值;DFEC
(2)如图2,设=m,CEBC=n(n<CFAC),若m+n=4mn,求证:PD=PC;12
(3)如图3,F为AC的中点,连接AE交CD于点Q,若QD=QP,直接写出的值.BEEC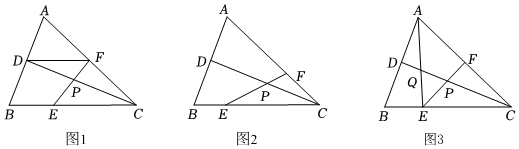 发布:2025/6/15 15:0:1组卷:334引用:2难度:0.3
发布:2025/6/15 15:0:1组卷:334引用:2难度:0.3 -
3.矩形ABCD中,AB=nAD(n>1),点P为对角线AC上的一个动点(不与A、C两点重合),过点P作直线MN⊥AC,分别交射线AB、射线AD于点M、N.
(1)如图1,当点N与点D重合时,求的值(用含有n的代数式表示).PMPD
(2)如图2,当点M为AB边的中点,且DP=DA时,求n的值.
(3)如图3,当n=2,移动点P,使得△APD与△BPC相似,则的值=.AMAD 发布:2025/6/15 15:0:1组卷:107引用:1难度:0.2
发布:2025/6/15 15:0:1组卷:107引用:1难度:0.2


