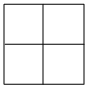
 操作与探索:将一张正方形纸片剪成四个大小、形状一样的小正方形(如图所示),记为第一次操作,然后将其中的一片又按同样的方法剪成四小片,记为第二次操作,如此循环进行下去.
操作与探索:将一张正方形纸片剪成四个大小、形状一样的小正方形(如图所示),记为第一次操作,然后将其中的一片又按同样的方法剪成四小片,记为第二次操作,如此循环进行下去.
(1)请将表中空缺的数据填写完整,并解答所提出的问题:
| 操作次数 | 1 | 2 | 3 | 4 | … |
| 正方形个数 | 4 | 7 |
10 10
|
13 13
|
… |
301
301
个正方形;(3)如果剪n次共能得到bn个正方形,则bn=
3n+1
3n+1
;(用含n的式子表示)(4)若原正方形的边长为1,设an表示第n次所剪的正方形的边长,则an=
()n
1
2
()n
;(用含n的式子表示)1
2
(5)在(4)的条件下,试猜想a1+a2+a3+a4+⋯+an-1+an与原正方形边长的数量关系.你猜想的结论是:a1+a2+a3+a4+⋯+an-1+an=
1-()n
1
2
1-()n
.(用含n的式子表示)1
2
【考点】规律型:图形的变化类;列代数式.
【答案】10;13;301;3n+1;()n;1-()n
1
2
1
2
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/10/8 17:0:1组卷:98引用:1难度:0.5
相似题
-
1.如图,在图1中,互不重叠的三角形共有4个,在图2中,互不重叠的三角形共有7个,在图3中,互不重叠的三角形共有10个,…,则在第n个图形中,互不重叠的三角形共有个 (用含n的代数式表示).
 发布:2025/6/17 4:30:1组卷:229引用:48难度:0.7
发布:2025/6/17 4:30:1组卷:229引用:48难度:0.7 -
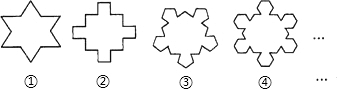
2.如图,①中多边形(边数为12)是由正三角形“扩展”而来的,②中多边形(边数为20)是由正方形“扩展”而来的….以此类推,由正n边形“扩展”而来的多边形的边为 .
 发布:2025/6/17 5:0:1组卷:134引用:37难度:0.7
发布:2025/6/17 5:0:1组卷:134引用:37难度:0.7 -
3.将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形有16个小圆,第4个图形有24个小圆,…,依此规律,第6个图形有
个圆.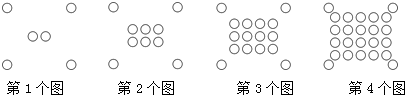 发布:2025/6/17 3:30:1组卷:1010引用:76难度:0.7
发布:2025/6/17 3:30:1组卷:1010引用:76难度:0.7


