定义：对任意一个两位数a,如果a满足个位数字与十位数字互不相同，且都不为零那么称这个两位数为“互异数”．将一个“互异数”的个位数字与十位数字对调后得到一个新的两位数，把这个新两位数与原两位数的和与11的商记为f（a）．例如：a=12，对调个位数字与十位数字得到新两位数21，新两位数与原两位数的和为21+12=33，和与11的商为33÷11=3，所以f（12）=3．根据以上定义，回答下列问题：
（1）①下列两位数：50，44，35中，“互异数”为 3535；
②计算：f（25）=77；
（2）一个“互异数”b的十位数字是m,个位数字是n,且m+n=5，求f（b）的值；
（3）如果一个“互异数”c的十位数字是2k+1，个位数字是k-2，且f（c）=8，求“互异数”c的值．
【答案】35；7
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/11 13:0:2组卷：131引用：3难度：0.5
相似题
-
1．长方形的长为a+2b,宽为a-b,那么其周长为（ ）
发布：2025/6/7 2:30:1组卷：16引用：2难度：0.7 -
2．若a-b=2，b-c=-5，则a-c=．
发布：2025/6/7 0:30:1组卷：388引用：9难度：0.8 -
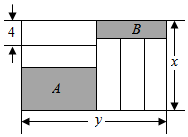3．如图，长为y（cm），宽为x（cm）的大长方形被分割为7小块，除阴影A，B外，其余5块是形状、大小完全相同的小长方形，其较短的边长为4cm,下列说法中正确的是（ ）
①小长方形的较长边为（y-12）cm；
②阴影A的较短边和阴影B的较短边之和为（x-y+4）cm；
③若x为定值，则阴影A和阴影B的周长和为定值；
④若y=20时，则阴影A的周长比阴影B的周长少8cm.发布：2025/6/6 16:30:1组卷：1180引用：4难度：0.5
