（1）如图1，在三角形ABC中，AC=BC=2，AB=23，求证：∠C=120°；
（2）如图2，已知菱形ABCD中，∠BAD=60°，AD=8，P、M分别为AC、AD上的两个动点（均不与A重合），且始终有PA=3AM，点N为菱形内部一点，连接MN交AC于点E，恰好∠PEN=60°，PE=2EN=2x,若用y表示阴影部分的面积之和，即y=S△PDM+S△ABN，回答下列两个问题：
①直接写出x的取值范围；
②求y与x的函数关系式，并求出阴影部分面积的最大值．
AB
=
2
3
PA
=
3
AM
【考点】四边形综合题．
【答案】（1）证明见解析过程；
（2）①；
②；阴影部分面积最大值为．
（2）①
0
＜
x
＜
4
3
3
②
y
=
-
3
3
x
2
+
18
x
9
3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/11 4:0:9组卷：23引用：2难度：0.5
相似题
-
1．如图，正方形ABCD的边长为4，点E在AB边上，BE=1，F为BC边的中点．将正方形截去一个角后得到一个五边形AEFCD，点P在线段EF上运动（点P可与点E，点F重合），作矩形PMDN，其中M，N两点分别在CD，AD边上．
设CM=x,矩形PMDN的面积为S．
（1）DM=（用含x的式子表示），x的取值范围是 ；
（2）求S与x的函数关系式；
（3）要使矩形PMDN的面积最大，点P应在何处？并求最大面积．发布：2025/6/20 10:0:1组卷：399引用：4难度：0.2 -
2．已知：在▱ABCD中，∠BAD=45°，AB=BD，E为BC上一点，连接AE交BD于F，过点D作DG⊥AE于G，延长DG交BC于H
（1）如图1，若点E与点C重合，且AF=，求AD的长；5
（2）如图2，连接FH，求证：∠AFB=∠HFB；
（3）如图3，连接AH交BF于M，当M为BF的中点时，请直接写出AF与FH的数量关系．发布：2025/6/20 10:30:1组卷：532引用：2难度：0.3 -
3．如图1，正方形ABCD，E为平面内一点，且∠BEC=90°，把△BCE绕点B逆时针旋转90°得△BAG，直线AG和直线CE交于点F．
（1）证明：四边形BEFG是正方形；
（2）若∠AGD=135°，猜测CE和CF的数量关系，并说明理由；
（3）如图2，连接DF，若AB=13，CF=17，求DF的长．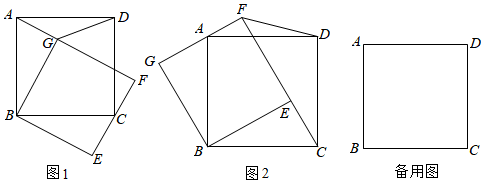
发布：2025/6/20 10:30:1组卷：97引用：1难度：0.1
