综合与实践
【问题情境】“漏壶”是一种古代计时器，在社会实践活动中，某小组同学根据“漏壶”的原理制作了如图①所示的液体漏壶，漏壶是由一个圆锥和一个圆柱组成的，中间连通，液体可以从圆锥容器中匀速漏到圆柱容器中，实验开始时圆柱容器中已有一部分液体．
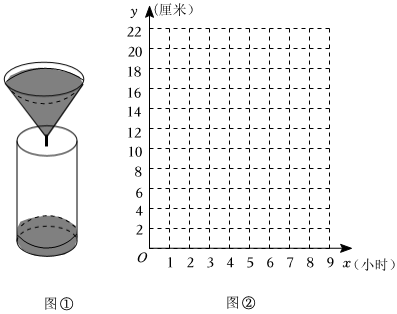
【实验观察】（1）下表是实验记录的圆柱体容器液面高度y（厘米）与时间x（小时）的数据：
| 时间x（小时） | 1 | 2 | 3 | 4 | 5 | |
| 圆柱体容器液面高度y（厘米） | 6 | 10 | 14 | 18 | 22 |
【探索发现】（2）请你根据表中的数据及图象，用所学过的一次函数、二次函数、反比例函数的知识确定y与x之间的函数解析式；
【结论应用】（3）如果本次实验记录的开始时间是上午9：00，那么当圆柱体容器液面高度达到12厘米时是几点？
【考点】一次函数的应用．
【答案】（1）见解析；
（2）y=4x+2；
（3）圆柱体容器液面高度达到12厘米时是上午11：30．
（2）y=4x+2；
（3）圆柱体容器液面高度达到12厘米时是上午11：30．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/15 8:0:8组卷：345引用：3难度：0.5
相似题
-
1．地表以下的岩层温度y随着所处深度x的变化而变化，在某个地点y与x的关系可以由公式y=35x+20来表示，则y随x的增大而（ ）
发布：2025/6/18 5:30:3组卷：184引用：11难度：0.9 -
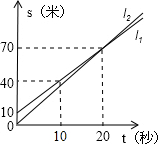2．小明和小强进行百米赛跑，小明比小强跑得快，如果两人同时起跑，小明肯定赢，如图所示，现在小明让小强先跑米，直线表示小明的路程与时间的关系，大约秒时，小明追上了小强，小强在这次赛跑中的速度是．发布：2025/6/18 5:30:3组卷：530引用：8难度：0.9 -
3．在一定范围内，弹簧的长度y（cm）与它所挂的物体的重量x（g）之间满足关系式y=kx+b,已知挂重50g时，弹簧长12.5cm,挂重200g时，弹簧长20cm,那么当弹簧长15cm时，挂重是（ ）
发布：2025/6/18 6:0:1组卷：316引用：6难度：0.9
