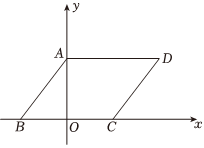
如图，▱ABCD在平面直角坐标系中，AD=6，若OA、OB的长是关于x的一元二次方程x2-7x+12=0的两个根，且OA＞OB．
（1）写出A、B两点的坐标．
（2）若E为x轴正半轴上的点，且S△AOE=163，求点E坐标，并判断△AOE与△DAO是否相似？
（3）若点M在平面直角坐标系内，则在直线AB上是否存在点F，使以A、C、
F、M为顶点的四边形为菱形？若存在，请直接写出其中两个F点的坐标；若不存在，请说明理由．
S
△
AOE
=
16
3
【考点】一次函数综合题．
【答案】（1）A（0，4），B（-3，0）；
（2）（，0）；△AOE∽△DAO；
（3）F1（-3，0），F2（3，8），F3（-，-），F4（-，）（任意两个F点即可）．
（2）（
8
3
（3）F1（-3，0），F2（3，8），F3（-
75
14
22
7
42
25
44
25
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/24 8:0:9组卷：46引用：1难度：0.2
相似题
-
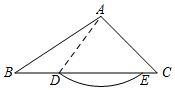1．在△ABC中，D是边BC上一点，以点A为圆心，AD长为半径作弧，如果与边BC有交点E（不与点D重合），那么称为△ABC的A-外截弧．ˆDE
例如，右图中是△ABC的一条A-外截弧．ˆDE
在平面直角坐标系xOy中，已知△ABC存在A-外截弧，其中点A的坐标为（5，0），点B与坐标原点O重合．
（1）在点C1（0，2），C2（5，-3），C3（6，4），C4（4，2）中，满足条件的点C是；
（2）若点C在直线y=x-2上，
①求点C的纵坐标的取值范围；
②直接写出△ABC的A-外截弧所在圆的半径r的取值范围．发布：2025/6/20 3:0:1组卷：291引用：5难度：0.4 -
2．如图，在平面直角坐标系xOy中，已知点A（3，1），B（2，3），C（2，1），将△ABC绕平面内的某个点P逆时针旋转α（0°＜α＜180°）角度后，得到△DEF，其中点A、B、的对应点为D（0，2）、E（-2，1）．
（1）在图中标出点P的位置，并画出旋转后的△DEF；
（2）旋转角α的度数为°；
（3）小宇尝试通过运用若干次轴对称变换来代替上面的旋转过程，他写出了一种变换的方法，将请将其补全：先将△ABC关于直线x=1对称，再将所得的图形再关于直线（填直线的表达式）对称得到△DEF．发布：2025/6/20 1:0:2组卷：16引用：1难度：0.3 -
3．已知在平面直角坐标系中，直线y=2x-8与x轴交于点A，与y轴交于点B．
（1）求A，B的坐标；
（2）平移线段AB，使得点A，B的对应点M，N分别落在直线l1：y=3x+6和直线l2：y=x+4上，求M，N的坐标；
（3）试证明直线y=kx+（1-k）恒平分四边形ABNM的面积，其中k≠0．12发布：2025/6/20 2:0:1组卷：862引用：3难度：0.4
