课本第30页介绍：美国总统伽菲尔德利用图1验证了勾股定理，直线l过等腰直角三角形ABC的直角顶点C；过点A作AD⊥l于点D，过点B作BE⊥l于点E研究图形，不难发现：△ADC≌△CEB．
（1）如图2，在平面直角坐标系中，等腰Rt△ACB，∠ACB=90°，AC=BC，点C的坐标为（0，-1），A点的坐标为（2，0），求B点坐标；
（2）如图3，在平面直角坐标系中，直线l1：y=2x+4分别与y轴，x轴交于点A，B，将直线l1绕点A顺时针或逆时针旋转45°得到l2，请任选一种情况求l2的函数表达式；
（3）如图4，在平面直角坐标系，点B（6，4），过点B作AB⊥y轴于点A，作BC⊥x轴于点C，P为线段BC上的一个动点，点Q（a,a+2）位于第一象限（且在AB上方）．问点A，P，Q能否构成以点Q为直角顶点的等腰直角三角形，若能，请直接写出Q点的坐标；若不能，请说明理由．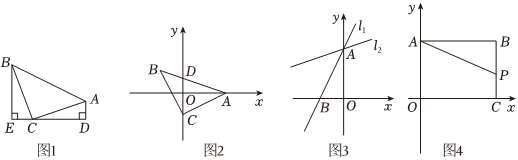
【考点】一次函数综合题．
【答案】（1）B（-1，1）；
（2）直线l2的解析式为：y=+4；
（3）Q（4，6）．
（2）直线l2的解析式为：y=
1
3
x
（3）Q（4，6）．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/10 8:0:9组卷：300引用：1难度：0.2
相似题
-
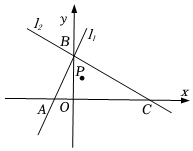1．如图，点P（a,a+2）是直角坐标系xOy中的一个动点，直线l1：y=2x+5与x轴，y轴分别交于点A，B，直线l2经过点B和点（6，2）并与x轴交于点C．
（1）求直线l2的表达式及点C的坐标；
（2）点P会落在直线l1：y=2x+5上吗？说明原因；
（3）当点P在△ABC的内部时．
①求a的范围；
②是否存在点P，使得∠OPA=90°？若存在，直接写出点P的坐标；若不存在，请说明理由．发布：2025/5/25 5:30:2组卷：374引用：2难度：0.4 -
2．如图1，在平面直角坐标系中，点O是坐标原点，直线y=-
x+12与y轴交于点A，与x轴交于B点，点C的坐标为（6，0）．34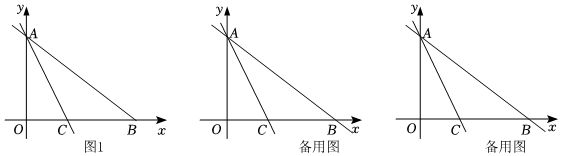
（1）求直线AC的解析式；
（2）点P为线段OC上一点，过点P作PD⊥OB，交AC于E，交AB于D，设点P横坐标为t,DE的长为d,求d与t的函数关系（不要求写出自变量t的取值范围）；
（3）在（2）的条件下，H为x轴负半轴上的一点，连接AH，EF⊥AH于点F，交y轴于点G，连接OF，若∠OFE=2∠OAC，d=，求点G的坐标．154发布：2025/5/25 2:30:1组卷：359引用：2难度：0.1 -
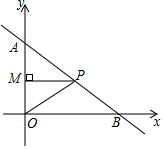3．如图：一次函数y=-x+3的图象与坐标轴交于A、B两点，点P是函数y=-34x+3（0＜x＜4）图象上任意一点，过点P作PM⊥y轴于点M，连接OP．34
（1）当AP为何值时，△OPM的面积最大？并求出最大值；
（2）当△BOP为等腰三角形时，试确定点P的坐标．发布：2025/5/25 1:0:1组卷：2719引用：3难度：0.3
