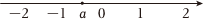观察下列各式的特征：|7-6|=7-6；|6-7|=7-6；
|
1
2
-
1
5
|
=
1
2
-
1
5
；
|
1
5
-
1
2
|
=
1
2
-
1
5
．根据规律，解决相关问题：
（1）把下列各式写成去掉绝对值符号的形式（不能写出计算结果）：
①|7-21|=
21-7
21-7
；
②|
7
17
-
7
18
|=
7
17
-
7
18
7
17
-
7
18
．
（2）当a＞b时，|a-b|=
a-b
a-b
；当a＜b时，|a-b|=
b-a
b-a
．
（3）有理数a在数轴上的位置如图，则化简|a-2|的结果为
C
C
．
A．a-2
B．a+2
C．2-a
D．-a-2
（4）计算：|
1
2
-1|+|
1
3
-
1
2
|+|
1
4
-
1
3
|+…+|
1
2020
-
1
2019
|．

【答案】21-7；

；a-b；b-a；C

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/9/7 2:0:9组卷：189引用：2难度：0.5

相似题

1．小明在做题的时候发现，两个连续正整数的积的倒数可以写成两个式子差的形式．
观察下面式子，完成以下问题：
1
1
×
2
=
1
-
1
2
，
1
2
×
3
=
1
2
-
1
3
，
1
3
×
4
=
1
3
-
1
4
，…
（1）请写出第15个式子：
；
（2）请用含n的式子表示第n个式子：
；
（3）计算：
1
1
×
2
+
1
2
×
3
+
1
3
×
4
+
⋯
+
1
2021
×
2022
；
（4）思考：如果不是两个连续正整数的积的倒数又如何去解决呢，请类比上题的方法计算：
1
1
×
3
+
1
3
×
5
+
1
5
×
7
+
⋯
+
1
2021
×
2023
．
发布：2025/6/8 13:30:1组卷：162引用：2难度：0.6
解析
2．观察等式：2+2²=2³-2，2+2²+2³=2⁴-2，2+2²+2³+2⁴=2⁵-2，…，已知按一定规律排列的一组数：2¹⁰⁰，2¹⁰¹，2¹⁰²，…，2¹⁹⁹，若2¹⁰⁰=m,用含m的代数式表示这组数的和是
．
发布：2025/6/8 14:0:2组卷：1442引用：13难度：0.6
解析
3．（1）用“＜”、“＞”、“=”填空：
5²+3²
2×5×3
3²+3²
2×3×3
（-3）²+2²
2×（-3）×2
（-4）²+（-4）²
2×（-4）×（-4）
（2）观察以上各式，你发现它们有什么规律吗？用一个含有字母的式子表示上述规律．
发布：2025/6/8 17:30:2组卷：126引用：3难度：0.7
解析

2．观察等式：2+22=23-2，2+22+23=24-2，2+22+23+24=25-2，…，已知按一定规律排列的一组数：2100，2101，2102，…，2199，若2100=m,用含m的代数式表示这组数的和是 ．