如图1，扇形AOB中，∠AOB=90°，OA=9，点P在半径OB上，连接AP．
（1）把△AOP沿AP翻折，点O的对称点为点Q．
①当点Q刚好落在弧AB上，求弧AQ的长；
②如图2，点Q落在扇形AOB外，AQ与弧AB交于点C，过点Q作QH⊥OA，垂足为H，探究OH、AH、QC之间的数量关系，并说明理由；
（2）如图3，记扇形AOB在直线AP上方的部分为图形W，把图形W沿着AP翻折，点B的对称点为点E，弧AE与OA交于点F，若OF=3，求PO的长．
【考点】圆的综合题．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/13 8:0:9组卷：190引用：1难度：0.5
相似题
-
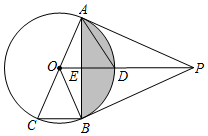1．如图，PA、PB是⊙O的切线，A、B是切点，AC是⊙O的直径，连接OP，交⊙O于点D，交AB于点E．
（1）求证：BC∥OP；
（2）若E恰好是OD的中点，且四边形OAPB的面积是16，求阴影部分的面积；3
（3）若sin∠BAC=，且AD=213，求切线PA的长．3发布：2025/5/23 16:0:1组卷：2045引用：7难度：0.1 -
2．【问题提出】
（1）如图①，AB为⊙O的一条弦，圆心O到弦AB的距离为4，若⊙O的半径为7，则⊙O上的点到弦AB的距离最大值为 ；
【问题探究】
（2）如图②，在△ABC中，∠BAC=60°，AD为BC边上的高，若AD=6，求△ABC面积的最小值；
【问题解决】
（3）“双减”是党中央、国务院作出的重大决策部署，实施一年多来，工作进展平稳，取得了阶段性成效，为了进一步落实双减政策，丰富学生的课余生活，某校拟建立一块综合实践基地，如图③，△ABC为基地的大致规划示意图，其中∠ABC=90°，BD平分∠ABC交AC于点D，点P为BC上一点，学校计划将四边形ABPD部分修建为农业实践基地，并沿BD铺设一条人行走道，△CDP部分修建为兴趣活动基地．根据规划要求，米，∠CDP=45°．且农业实践基地部分（四边形ABPD）的面积应尽可能小，问四边形ABPD的面积是否存在最小值？若存在，求出其最小值；若不存在，请说明理由．BD=802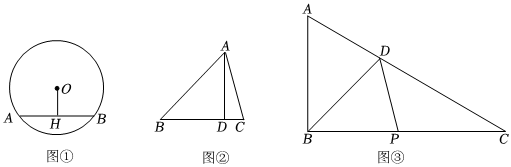
发布：2025/5/23 16:0:1组卷：251引用：1难度：0.3 -
3．AB、AC为圆O的弦，OA平分∠BAC．
（1）如图1，求证：弧AB=弧AC；
（2）如图2，连接BO并延长交圆O于点F，连接AF，作BG⊥AC于点G，延长AO交BG于点M，求证：AF=BM；
（3）如图3，在（2）的条件下，连接OG，延长BG交圆O于点D，连接CD并延长，与AF的延长线交于点K，AB=2FK，BC=6，求OG的长．
发布：2025/5/23 16:30:1组卷：112引用：1难度：0.2
