如图1是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图2的形状拼成一个正方形．
（1）图2中的阴影部分的正方形的边长等于 m-nm-n；
（2）请用两种不同的方法求图2中阴影部分的面积．
方法一：（m-n）2（m-n）2；
方法二：（m+n）2-4mn（m+n）2-4mn；
（3）观察图2你能写出下列三个代数式之间的等量关系吗？代数式（m+n）2，（m-n）2，mn,（m-n）2=（m+n）2-4mn（m-n）2=（m+n）2-4mn；
（4）根据（3）题中的等量关系，解决如下问题：若a+2b=7，ab=5，求（a-2b）2的值；
（5）拓展：若（m-2021）2+（2022-m）2=15，求（m-2021）（2022-m）的值．
【考点】完全平方公式的几何背景；多项式乘多项式．
【答案】m-n；（m-n）2；（m+n）2-4mn；（m-n）2=（m+n）2-4mn
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/14 8:0:9组卷：268引用：1难度：0.4
相似题
-
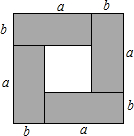1．利用图形面积可以解释代数恒等式的正确性，也可以解释不等式的正确性．
（1）根据下列所示图形写出一个代数恒等式；
（2）已知正数a,b,c和m,n,l,满足a+m=b+n=c+l=k.试构造边长为k的正方形，利用图形面积来说明al+bm+cn＜k2．发布：2025/5/27 15:0:2组卷：268引用：7难度：0.7 -
2．如图，有两个正方形纸板A，B，纸板A与B的面积之和为34．现将纸板B按甲方式放在纸板A的内部，阴影部分的面积为4．若将纸板A，B按乙方式并列放置后，构造新的正方形，则阴影部分的面积为（ ）
发布：2025/5/26 7:30:2组卷：414引用：8难度：0.6 -
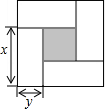3．如图所示的是用4个全等的小长方形与1个小正方形密铺而成的正方形图案，已知该图案的面积为49，小正方形的面积为4，若分别用x,y（x＞y）表示小长方形的长和宽，则下列关系式中不正确的是（ ）发布：2025/5/26 12:0:1组卷：1034引用：8难度：0.7
