已知正方形ABCD，M是AB中点，E是AB延长线上一点，NM⊥DM，且交∠CBE的角平分线于点N，如图1，
（1）证明：DM=MN．
（2）若将上述条件中的“M是AB的中点”改成“M是AB上的任意一点”其余条件不变，如图2，则结论DM=MN还成立吗？如果成立，请证明；若不成立，请说明理由．
【考点】正方形的性质；全等三角形的判定与性质．
【答案】（1）证明见解答过程；
（2）M是AB上的任意一点，DM=MN还成立，证明见解答过程．
（2）M是AB上的任意一点，DM=MN还成立，证明见解答过程．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/30 10:0:2组卷：46引用：1难度：0.4
相似题
-
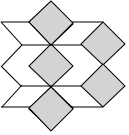1．如图所示是由形状大小相同的菱形地砖、正方形地砖铺设的地面图案的一部分，现已知每块正方形地砖的面积为6400cm2，则每块菱形地砖的面积为 cm2．发布：2025/6/18 5:0:1组卷：135引用：5难度：0.8 -
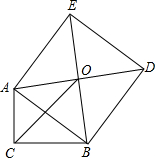2．如图，Rt△ABC中，∠C=90°，以斜边AB为边向外作正方形ABDE，且正方形对角线交于点O，连接OC，已知AC=5，OC=6，则另一直角边BC的长为2．发布：2025/6/18 5:30:3组卷：7311引用：30难度：0.5 -
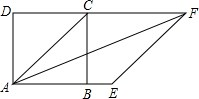3．如图，以正方形ABCD的对角线AC为一边作菱形AEFC，则∠FAB=．发布：2025/6/18 6:0:1组卷：358引用：12难度：0.7
