如图，在▱ABCD中，AC是对角线，∠BAC=90°，∠ABC=45°，BC=16．点P、Q分别是线段AD，射线CB上的一点，CQ=2AP，点E是线段CQ上的点，且QE=4，设AP=m（m＞2）．
（1）CQ=2m2m，CE=2m-42m-4；（用含m的代数式表示）
（2）①若PE⊥BC，求m的值；
②在①条件下，判断四边形APEQ的形状，并说明理由；
（3）当点P关于直线AE的对称点恰好落在直线AB上时，直接写出m的值．
【答案】2m；2m-4
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/28 8:0:9组卷：95引用：2难度：0.5
相似题
-
1．如图，在平行四边形ABCD中，点E、F分别在边BC和AD上，且BE=DF．求证：AE∥CF．发布：2024/12/23 19:30:2组卷：1085引用：15难度：0.7 -
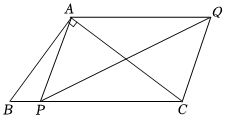2．如图，在Rt△ABC中，∠BAC=90°，AB=6，BC=10，P为BC边上任意一点（点P与点C不重合），连接PA，以PA，PC为邻边作平行四边形PAQC，连接PQ，则PQ长的最小值是 ．发布：2025/1/28 8:0:2组卷：510引用：3难度：0.6 -
3．如图所示，在▱ABCD中，对角线AC与BD相交于点O，过点O任作一条直线分别交AB、CD于点E、F．
（1）求证：OE=OF；
（2）若AB=7，BC=5，OE=2，求四边形BCFE的周长．发布：2024/12/23 19:30:2组卷：1015引用：9难度：0.7
