阅读下面材料，并完成相应的任务．
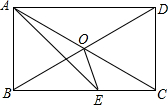
三等分角是古希腊三大几何问题之一．如图，任意∠ABC可被看作是矩形ACBD的对角线BA与边BC的夹角，以点B为端点的射线BF交AC于点E，交DA的延长线于点F．若EF=2AB，则∠CBF是∠ABC的一个三等分角．
证明：如图，取EF的中点G，连接AG．
∵四边形ACBD是矩形，∴∠DAC=90°，AD∥BC．∴∠EAF=180°-∠DAC=90°．
在Rt△AEF中，∵点G是EF的中点，∴AG=

1

2

EF，FG=

1

2

EF，AG=FG．
……
任务一：上面证明过程中得出“AG=

1

2

EF”的依据是

直角三角形斜边上的中线等于斜边的一半

直角三角形斜边上的中线等于斜边的一半

；
任务二：完成材料证明中的剩余部分．