如图1和图2，在△ABC中，AB=AC=10，BC=16，点M，N分别在AB，BC上，且AM=CN=4．点P从点M出发沿折线MB-BN匀速运动，到达点N后停止运动，点Q从点C出发沿线段AC匀速运动，到A点后立即以原速返回．两点同时出发，当其中一个点到达终点后，另一点随之停止运动．已知P，Q运动速度均为每秒2个单位长度，运动时间为t秒．
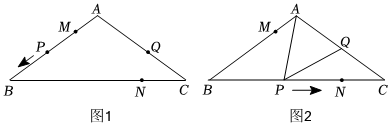
（1）求S△ABC；
（2）当点P在线段BM上运动时，若AP=AQ，求t的值；
（3）①当点P在线段BM上运动时，设点P到BC的距离为x,试用含x的代数式表示点P到边AC所在直线的距离 48-8x548-8x5；
②当点P在线段BN上运动时，设点P到AB的距离为x,试用含x的代数式表示点P到边AC所在直线的距离 48-5x548-5x5；
（4）在点Q从点A向点C运动过程中，直接写出t=88秒时，△APQ面积最大，此时S△APQ=10.810.8．
48
-
8
x
5
48
-
8
x
5
48
-
5
x
5
48
-
5
x
5
【考点】三角形综合题．
【答案】；；8；10.8
48
-
8
x
5
48
-
5
x
5
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/18 8:0:9组卷：36引用：2难度：0.5
相似题
-
1．已知AB=BC，∠ABC=90°，直线l是过点B的一条动直线（不与直线AB，BC重合），分别过点A，C作直线l的垂线，垂足为D，E．
（1）如图1，当45°＜∠ABD＜90°时，
①求证：CE+DE=AD；
②连接AE，过点D作DH⊥AE于H，过点A作AF∥BC交DH的延长线于点F．依题意补全图形，用等式表示线段DF，BE，DE的数量关系，并证明；
（2）在直线l运动的过程中，若DE的最大值为3，直接写出AB的长．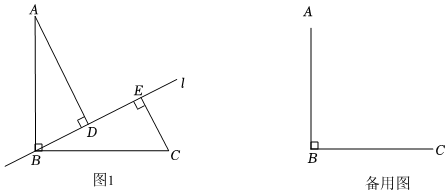
发布：2025/5/23 20:30:1组卷：1374引用：5难度：0.4 -
2．课本再现
如图1，在等边△ABC中，E为边AC上一点，D为BC上一点，且AE=CD，连接AD与BE相交于点F．
（1）AD与BE的数量关系是 ，AD与BE构成的锐角夹角∠BFD的度数是 ；
深入探究
（2）将图1中的AD延长至点G，使FG=BF，连接BG，CG，如图2所示．求证：GA平分∠BGC．（第一问的结论，本问可直接使用）
迁移应用
（3）如图3，在等腰△ABC中，AB=AC，D，E分别是边BC，AC上的点，AD与BE相交于点F．若∠BAC=∠BFD，且BF=3AF，求值．BDCD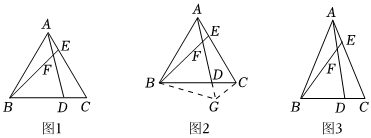
发布：2025/5/23 20:30:1组卷：1077引用：3难度：0.1 -
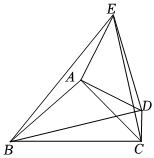3．如图，在△ABC中，AB=AC=3，∠BAC=90°，点D为一个动点，且点D到点C的距离为1，连接CD，AD，作EA⊥AD，使AE=AD．
（1）求证：△ADB≌△AEC；
（2）求证：BD⊥EC；
（3）直接写出BD最大和最小值；
（4）点D在直线AC上时，求BD的长．发布：2025/5/23 21:0:1组卷：103引用：2难度：0.4
