【问题情境】
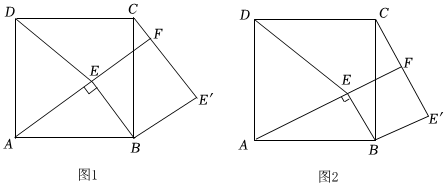
如图1，点E为正方形ABCD内一点，∠AEB=90°，将Rt△ABE绕点B按顺时针方向旋转90°，得到△CBE′（点A的对应点为点C）．延长AE交CE′于点F，连接DE．
（1）试判断四边形BE'FE的形状，并说明理由；
【解决问题】
（2）若CF=3，BE=3CF，请求出正方形ABCD的面积；
【猜想证明】
（3）如图2，若DA=DE，请猜想线段CF与FE'的数量关系并加以证明．
【考点】四边形综合题．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/31 1:0:8组卷：127引用：3难度：0.3
相似题
-
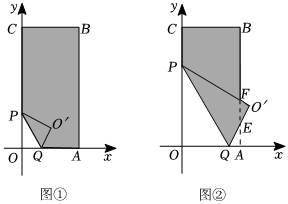1．将一个矩形纸片OABC放置在平面直角坐标系中，点O（0，0），点A（3，0），点C（0，6），点P在矩形的边OC上，折叠该纸片，使折痕所在的直线经过点P，并与x轴的正半轴相交于点Q，且∠OPQ=30°，点O的对应点O'落在第一象限．设O′Q=t.
（Ⅰ）如图①，当t=1时，求∠O′QA的大小和点O′的坐标；
（Ⅱ）如图②，若折叠后重合部分为四边形，O′Q，O'P分别与边AB相交于点E，F，试用含有t的式子表示重叠部分的面积S，并写出t的取值范围；
（Ⅲ）当折痕PQ恰好过点A时，求折叠后重合部分的面积 ．发布：2025/5/23 17:0:1组卷：311引用：1难度：0.1 -
2．如图，在△ABC中，∠ABC=30°，AB=AC，点O为BC的中点，点D是线段OC上的动点（点D不与点O，C重合），将△ACD沿AD折叠得到△AED，连接BE．
（1）当AE⊥BC时，∠AEB=°；
（2）探究∠AEB与∠CAD之间的数量关系，并给出证明；
（3）设AC=4，△ACD的面积为x,以AD为边长的正方形的面积为y,求y关于x的函数解析式．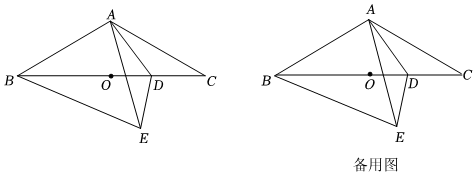
发布：2025/5/23 17:30:1组卷：977引用：7难度：0.5 -
3．【基础巩固】（1）如图1，在△ABC中，D，E分别在AB，BC上，∠BDE=∠C，求证：BD⋅BA=BE⋅BC．
【尝试应用】（2）如图2，在△ABC中，D，E，F分别在AB，BC，CA上，四边形ADEF为平行四边形，∠DFE=∠C，AD=4，BD=2，求AC的长．
【拓展提高】（3）如图3，平行四边形ABCD的周长为10，E，G分别在AC，AD上，四边形ECFG为平行四边形，CE=4AE，∠B=2∠CEF=2∠AGE，求EF的长．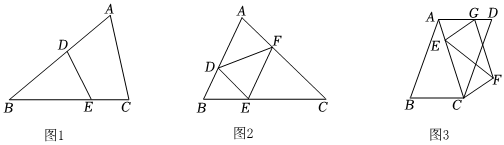
发布：2025/5/23 17:30:1组卷：334引用：1难度：0.3
