如图，在平面直角坐标系中，已知抛物线y=x2+bx+c与直线AB相交于A，B两点，其中A（-3，-4），B（0，-1）．
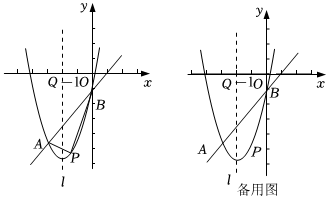
（1）求该抛物线的函数表达式；
（2）点P为直线AB下方抛物线上的任意一点，连接PA，PB，是否存在点P，使△PAB面积最大，若存在，求出△PAB最大面积，若不存在，请说明理由．
【答案】（1）y=x2+4x-1；
（2）存在，．
（2）存在，
27
8
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/31 7:0:9组卷：20引用：2难度：0.4
相似题
-
1．根据条件求函数的关系式
（1）已知二次函数y=x2+bx+c经过（-2，5）和（2，-3）两点，求该函数的关系式；
（2）已知二次函数的图象以A（-1，4）为顶点，且过点B（2，-5），求该函数的关系式．发布：2025/6/6 19:30:1组卷：240引用：2难度：0.5 -
2．抛物线y=-x2+bx+c的顶点坐标是（1，-2），则该抛物线的解析式是 ．
发布：2025/6/3 16:30:1组卷：1099引用：4难度：0.7 -
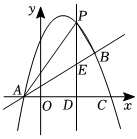3．如图，抛物线y=ax2+bx+c（a≠0）与直线y=x+1交于A（-1，0），B（4，n）两点，且抛物线经过点C（5，0）．
（1）求抛物线的解析式；
（2）点P是直线上方的抛物线上的一个动点，求△ABP的面积最大时的P点坐标．发布：2025/6/4 14:0:1组卷：307引用：3难度：0.5
