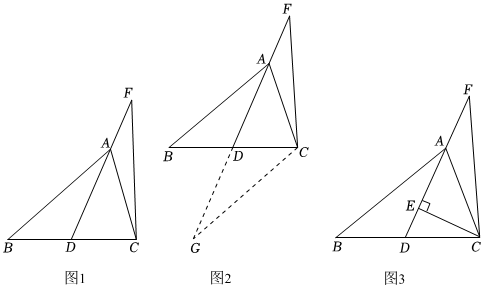
如图,在△ABC中,AD为BC边上的中线,在DA延长线上找一点F,使得CF=AB.
(1)求证:∠F=∠BAD;
完成下面的证明过程:
证明:过点C作CG∥AB,交AD的延长线于点G.如图2,
∴∠G=∠BAD,
∵AD为BC边上的中线,
∴BD=CD.
在△ADB和△GDC中,
∵∠BAD=∠G ∠ADB=∠GDC BD=CD
,
∴△ADB≌△GDC(AAS).
∴AB=CGAB=CG.
又∵CF=AB,
∴CF=CGCF=CG.
∴∠G=∠F∠G=∠F.
∵∠G=∠BAD,
∴∠F=∠BAD.
(2)过点C作CE⊥AD于点E,如图3.用等式表示线段AF、DE之间的数量关系,并证明.
∠ BAD =∠ G |
∠ ADB =∠ GDC |
BD = CD |
【考点】全等三角形的判定与性质.
【答案】AB=CG;CF=CG;∠G=∠F
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/10/10 1:0:2组卷:219引用:1难度:0.5
相似题
-
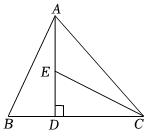 1.在△ABC中,AD⊥BC于点D,点E为AD上一点,连接CE,CE=AB,ED=BD.
1.在△ABC中,AD⊥BC于点D,点E为AD上一点,连接CE,CE=AB,ED=BD.
(1)求证:△ABD≌△CED;
(2)若∠ACE=22°,则∠B的度数为 .发布:2025/6/15 23:30:1组卷:561引用:8难度:0.5 -
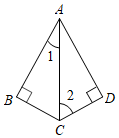 2.如图,∠B=∠D=90°,AB=AD,∠2=64°,则∠1=°.发布:2025/6/15 23:30:1组卷:260引用:3难度:0.8
2.如图,∠B=∠D=90°,AB=AD,∠2=64°,则∠1=°.发布:2025/6/15 23:30:1组卷:260引用:3难度:0.8 -
3.如图,将两个全等的直角三角形△ABD、△ACE拼在一起(图1),△ABD不动.
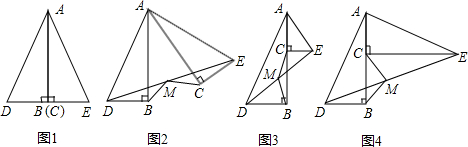
(1)若将△ACE绕点A逆时针旋转,连接DE,M是DE的中点,连接MB、MC(图2),证明:MB=MC.
(2)若将图1中的CE向上平移,∠CAE不变,连接DE,M是DE的中点,连接MB、MC(图3),判断并直接写出MB、MC的数量关系.
(3)在(2)中,若∠CAE的大小改变(图4),其他条件不变,则(2)中的MB、MC的数量关系还成立吗?说明理由.发布:2025/6/15 23:0:1组卷:18634引用:9难度:0.3


