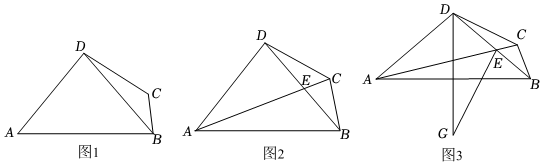
已知：如图1，在四边形ABCD中，连接BD，∠ADB=180°-2∠A．
（1）求证：AD=BD；
（2）如图2，连接AC，交BD于点E，若∠BCD+∠DCE=180°．求证：∠CBD=∠CAD；
（3）如图3，在（2）的条件下，点G为四边形ABCD外一点，连接GE、GD，且满足∠GEA=∠GDA，∠AEG+∠CBD+∠BDC=90°，若BC+CE=DE，CD=14，GD-GE=2，求△DCE的面积．
14
2
【考点】四边形综合题．
【答案】（1）证明见解答过程；
（2）证明见解答过程；
（3）．
（2）证明见解答过程；
（3）
7
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/14 1:0:1组卷：40引用：2难度：0.3
相似题
-
1．如图，在Rt△ABC中，∠C=90°，AC=16厘米，BC=20厘米，点D在BC上，且CD=12厘米．现有两个动点P，Q分别从点A和点B同时出发，其中点P以4厘米/秒的速度沿AC向终点C运动；点Q以5厘米/秒的速度沿BC向终点C运动．过点P作PE∥BC交AD于点E，连接EQ．设动点运动时间为t秒（t＞0）．
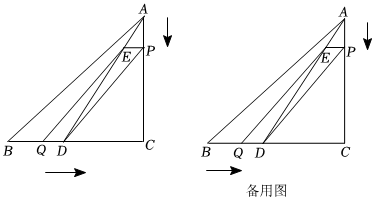
（1）CP=；（用t的代数式表示）
（2）连接CE，并运用割补的思想表示△AEC的面积（用t的代数式表示）；
（3）是否存在某一时刻t,使四边形EQDP是平行四边形，如果存在，请求出t,如果不存在，请说明理由；
（4）当t为何值时，△EDQ为直角三角形．发布：2025/6/7 17:0:1组卷：348引用：3难度：0.1 -
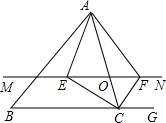2．如图，在△ABC中，点O是AC边上一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于点E，交△BCA的外角∠ACG的平分线于点F．
（1）探究OE与OF的数量关系并加以以证明；
（2）连接BE，BF，当点O在边AC上运动时，四边形BCFE可能为菱形吗？若可能，请证明；若不可能，请说明理由；
（3）连接AE，AF，当点O在AC上运动到什么位置时，四边形AECF是矩形？请说明理由；
（4）在（3）的条件下，△ABC满足什么条件时，四边形AECF是正方形？请说明理由．发布：2025/6/7 17:0:1组卷：299引用：2难度：0.4 -
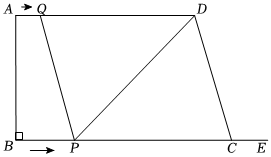3．如图，在四边形ABCD中，AD∥BC，∠B=90°，AD=16cm,AB=12cm,BC=21cm,动点P从点B出发，沿射线BC的方向以每秒2cm的速度运动到C点返回，动点Q从点A出发，在线段AD上以每秒1cm的速度向点D运动，点P，Q分别从点B，A同时出发，当点Q运动到点D时，点P随之停止运动，设运动的时间t（秒）．
（1）求DQ、PC的代数表达式；
（2）当t为何值时，四边形PQDC是平行四边形；
（3）当0＜t＜10.5时，是否存在点P，使△PQD是等腰三角形？若存在，请直接写出所有满足要求的t的值；若不存在，请说明理由．发布：2025/6/7 16:30:2组卷：243引用：5难度：0.2
