在平面直角坐标系中，四边形OABC的顶点A、C分别在x轴和y轴上，顶点B在第一象限，OA∥CB．
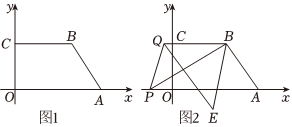
（1）如图1，已知OC=3，点A（6，0），B（4，3），点C的坐标是

（0，3）

（0，3）

．
（2）在（1）的条件下，点M是y轴上一点．且

S

△

BCM

=

2

3

S

△

AOM

，求点M的坐标；
（3）如图2，点P是x轴上点A左边的一点，点Q是射线BC上一点，连接PB、PQ，∠ABP和∠BQP的平分线相交于点E，求

∠

BAP

+

∠

BPQ

∠

BEQ

的值（可以直接利用三角形内角和等于180度）．