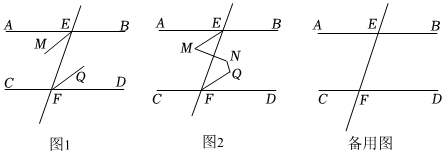
如图1，AB∥CD，直线EF与AB、CD相交于点E、F，EM平分∠AEF，FQ平分∠EFD．
（1）求证：EM∥FQ；
（2）如图2，N为EM、FQ之间一点（∠M＜∠Q），若∠N+∠Q=240°，求∠M的度数；
（3）若G为直线CD下方一点，∠GFD=12∠EFD，H为直线EF右侧一点，满足GH⊥MH，则∠EMH、∠FGH、∠AEF之间满足的数量关系是 ∠AEF+∠FGH-∠EMH=90°∠AEF+∠FGH-∠EMH=90°．
∠
GFD
=
1
2
∠
EFD
【考点】平行线的判定与性质．
【答案】∠AEF+∠FGH-∠EMH=90°
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/28 8:0:9组卷：856引用：1难度：0.3
