【概念认识】城市的许多街道是相互垂直或平行的，因此往往不能沿直线行走到目的地，只能按直角拐弯的方式行走．我们可以按照街道的垂直和平行方向建立平面直角坐标系xOy,对两点A（x1，y1）和B（x2，y2），用以下方式定义两点间的“折线距离”：d（A，B）=|x1-x2|+|y1-y2|．
【数学理解】
（1）①已知点A（-3，1），则d（O，A）=44；
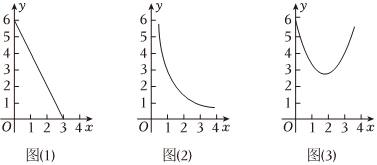
②函数y=-2x+6（0≤x≤3）的图象如图（1），B是图象上一点，若d（O，B）=5，则点B的坐标为 （1，4）（1，4）；
（2）函数y=3x（x＞0）的图象如图（2），该函数图象上是否存在点C，使d（O，C）=2？若存在，求出其坐标；若不存在，请说明理由；
【拓展运用】
（3）函数y=x2-4x+6（x≥0）的图象如图（3），D是图象上一点，求d（O，D）的最小值及对应的点D的坐标．
y
=
3
x
（
x
＞
0
）
【考点】二次函数综合题．
【答案】4；（1，4）
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/19 8:0:9组卷：220引用：1难度：0.7
相似题
-
1．在平面直角坐标系中，∠ACB=90°，AB∥x轴，如图1，C（1，0），且OC：OA=AC：BC=1：2．
（1）求点A、点B的坐标；
（2）已知抛物线y=ax2+bx+c（a≠0）过A、B、C三点，求该抛物线的表达式；
（3）如图2，抛物线对称轴与AB交于点D，现有一点P从点A出发，以每秒1个单位的速度在AB上向点B运动，另一点Q从点D与点P同时出发，以每秒5个单位在抛物线对称轴上运动．当点P到达B点时，点P、Q同时停止运动，问点P、Q运动到何处时，△PQB面积最大，并求出最大面积．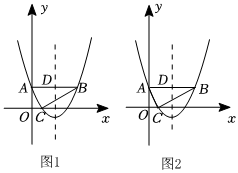
发布：2025/5/23 20:0:1组卷：276引用：2难度：0.1 -
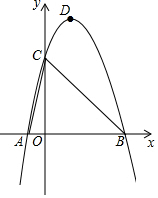2．如图，在平面直角坐标系中，抛物线y=ax2+bx+c经过A（-1，0），B（4，0），C（0，4）三点．
（1）求抛物线的解析式及顶点D的坐标；
（2）将（1）中的抛物线向下平移个单位长度，再向左平移h（h＞0）个单位长度，得到新抛物线．若新抛物线的顶点D′在△ABC内，求h的取值范围；154
（3）点P为线段BC上一动点（点P不与点B，C重合），过点P作x轴的垂线交（1）中的抛物线于点Q，当△PQC与△ABC相似时，求△PQC的面积．发布：2025/5/23 20:30:1组卷：3026引用：2难度：0.1 -
3．已知抛物线y=x2-（m+1）x+m2-2．
（1）当m=1时，求此抛物线的对称轴和顶点坐标；
（2）若该抛物线y=x2-（m+1）x+m2-2与直线y1=x+2m+1的一个交点P在y轴正半轴上．
①求此抛物线的解析式；
②当n≤x≤n+1时，求y的最小值（用含n的式子表示）．发布：2025/5/23 20:30:1组卷：435引用：2难度：0.5
