【问题探究】
某学习小组同学按照以下思路研究不等式组-1≤-|x|+3≤2的解集：
首先令y=-|x|+3，通过列表、描点、连线的方法作出该函数的图象并对其性质进行探究．
列表：

x	…	-4	-3	-2	-1	0	1	2	3	4	…
y	…	-1 -1	0 0	1 1	2 2	3 3	2 2	1 1	0 0	-1 -1	…

描点与连线：
​
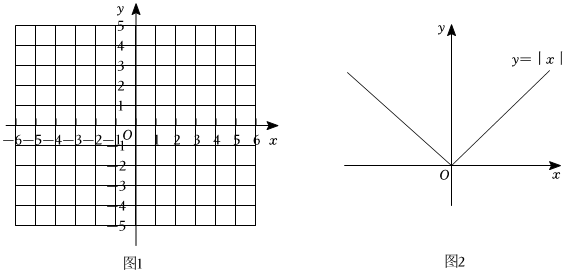
（1）在列表的空格处填对应的y值，在图1给出的平面直角坐标系中描出以表中各对应值为坐标的点，并根据描出的点，画出该函数的图象；
（2）若P（a,b），Q（5，b）为该函数图象上不同的两点，则a=

-5

-5

；
（3）观察图象，当-1≤-|x|+3≤2时，自变量x的取值范围是

-4≤x≤-1或1≤x≤4

-4≤x≤-1或1≤x≤4

；
【拓展运用】
函数y=|x|的图象如图2所示，在同一平面直角坐标系中画出函数

y

=

-

1

2

x

+

3

的图象草图，并求出它与函数y=|x|的图象所围成的图形面积．