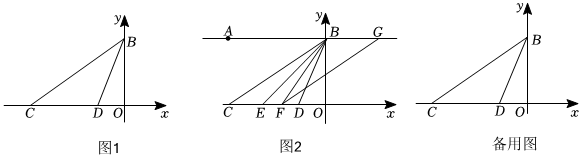
平面直角坐标系中,点C、D在x轴负半轴上,点B在y轴正半轴上,OB=b,OC=c,OD=d,且(b-6)2+|c-9|+52-d=0.
(1)求B、C、D三点的坐标;
(2)若点P在y轴上,且三角形BPD的面积是三角形BCD面积的56,求点P坐标;
(3)过点B作AB∥x轴,已知CB平分∠ABD,点E是x轴上的一个动点(不与点C,D重合),BF平分∠DBE交直线CD于点F,过点F作GF∥BC交直线AB于点G.
①如图2,当点E在点D的左侧,且∠BFG=30°时,求∠BEF的值;
②直接写出∠BFG和∠BEF之间的数量关系.
(
b
-
6
)
2
+
|
c
-
9
|
+
5
2
-
d
=
0
5
6
【答案】(1)B(0,6),C(-9,0),D(-,0);
(2)P坐标为(0,19)或(0,-7);
(3)①60°;
②当点E在点D的左侧,∠BEF=2∠BFG;当点E在点D的右侧,∠BEF=180°-2∠BFG.
5
2
(2)P坐标为(0,19)或(0,-7);
(3)①60°;
②当点E在点D的左侧,∠BEF=2∠BFG;当点E在点D的右侧,∠BEF=180°-2∠BFG.
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/6/19 8:0:9组卷:215引用:1难度:0.2