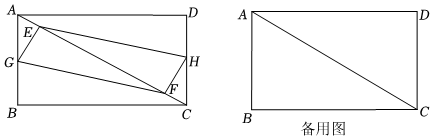
如图，矩形ABCD中，AB=6cm,BC=8cm,E、F是对角线AC上的两个动点，分别从A、C同时出发，相向而行，速度均为2cm/s,运动时间为t（0≤t≤5）秒．
（1）若G、H分别是AB、DC的中点，且t≠2.5s,求证：以E、G、F、H为顶点的四边形始终是平行四边形；
（2）在（1）的条件下，当t为何值时？以E、G、F、H为顶点的四边形是矩形；
（3）若G、H分别是折线A-B-C，C-D-A上的动点，分别从A、C开始，与E、F相同的速度同时出发，当t为何值时，以E、G、F、H为顶点的四边形是菱形，请直接写出t的值．
【考点】四边形综合题．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/27 10:35:59组卷：774引用：9难度：0.1
相似题
-
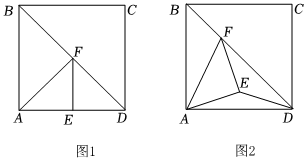1．在正方形ABCD中，AB=4，F为对角线BD上一动点，连接AF，以AF为斜边向右下方作等腰直角△AFE，连接DE．2
（1）如图1，当点E落在线段AD上时，求证：AE=ED；
（2）如图2，当点E不在线段AD上时，判断（1）中的结论是否成立，若成立，请证明；若不成立，请说明理由；
（3）当DE=时，求线段BF的长；522
（4）若点F从点B运动到点D，直接写出点E经过的路径长．发布：2025/5/24 21:0:1组卷：129引用：1难度：0.2 -
2．知识再现：已知，如图1，四边形ABCD是正方形，点M、N分别在边BC、CD上，连接AM、AN、MN，且∠MAN=45°，延长CB至G使BG=DN，连接AG，根据三角形全等的知识，我们可以证明MN=BM+DN．
知识探究：（1）如图1，作AH⊥MN，垂足为点H，猜想AH与AB有什么数量关系？并进行证明．
知识运用：（2）如图2，四边形ABCD是正方形，E是边BC的中点，F为边CD上一点，且∠FEC=2∠BAE，AB=24，求DF的长．
知识拓展：（3）已知∠BAC=45°，AD⊥BC于点D，且BD=2，AD=6，求CD的长．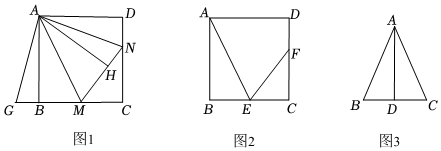
发布：2025/5/24 21:0:1组卷：268引用：2难度：0.4 -
3．已知：线段EF和矩形ABCD如图①摆放（点E与点B重合），点F在边BC上EF=1cm,AB=4cm,BC=8cm.如图②．EF从图①的位置出发，沿BC方向运动，速度为1cm/s；动点P同时从点D出发，沿DA方向运动，速度为1cm/s.点M为AB的中点，连接PM，ME，DF，PM与AC相交于点Q，设运动时间为（s）（0＜1≤7）．解答下列问题：
（1）当PM⊥AC时，求r的值；
（2）设五边形PMEFD的面积为S（cm2），求S与t的关系式；
（3）当ME∥AC时，求线段AQ的长；
（4）当t为何值时，五边形DAMEF的周长最小，最小是多少？直接写出答案即可）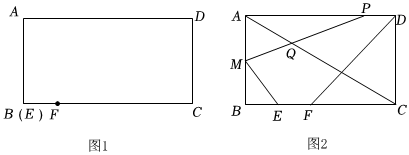
发布：2025/5/24 21:0:1组卷：133引用：1难度：0.1
