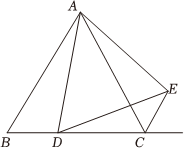
如图，△ABC是等边三角形，且AB=2，点D在线段BC上．以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．
（1）求证：∠BCE+∠BAC=180°，
（2）当四边形ADCE的周长取最小值时，求BD的长．

【答案】（1）见解答；
（2）1．

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/9/27 13:0:2组卷：236引用：1难度：0.5

相似题

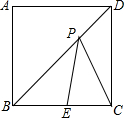1．在正方形ABCD中，E在BC上，BE=2，CE=1，P在BD上，则PE和PC的长度之和最小可达到

．
发布：2025/6/15 18:0:1组卷：161引用：4难度：0.7
解析
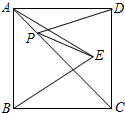2．如图所示，正方形ABCD的面积为16，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为（　　）
A．2 B．2
6
C．3 D．4
发布：2025/6/15 19:0:1组卷：486引用：8难度：0.9
解析
3．如图，矩形ABCD中，AB=2，对角线AC、BD交于点O，∠AOD=120°，E为BD上任意点，P为AE中点，则PO+PB的最小值为（　　）
A．
3
B．1+
3
C．
7
D．3
发布：2025/6/15 19:30:1组卷：872引用：6难度：0.4
解析

如图，△ABC是等边三角形，且AB=2，点D在线段BC上．以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．（1）求证：∠BCE+∠BAC=180°，（2）当四边形ADCE的周长取最小值时，求BD的长．