在《车轮为什么是圆的》课题学习中，小青将车轮设计成半径为2的正n多边形，在水平地面上模拟行驶．以n=3为例，如图1，车轮转动一次（以一个顶点为支点旋转），车轮中心的轨迹是BD，点C为中心轨迹最高点（即

ˆ

BD

的中点），转动一次前后中心的连线是BD（水平线），如图2，d为点C到BD的距离（即CE的长）．当n取4，5，6时，车轮中心的轨迹分别如图3、图4、图5．

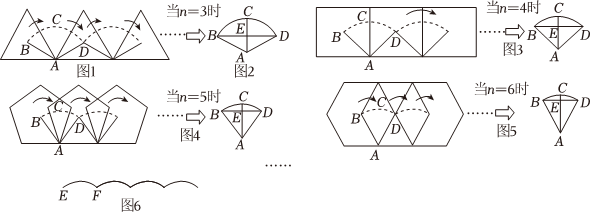
以此类推，当n取不同的值时，分别计算出d的值（结果精确到0.001）．具体数据如下表：

n	3	4	5	6	7	8	9	10	11	⋯
d	1.000		0.382	0.268	0.198	0.152	0.121	0.098	0.081	⋯

请你协助小青完成以下任务．
（1）求当n=4时，d为何值？（参考数据：

2

≈

1

.

414

）

（2）根据表格数据，d随n的变化情况为

d随n的增大而减小

d随n的增大而减小

；当车轮设计成圆形时，d=

0

0

，这样车辆行驶平稳、没有颠簸感．所以，将车轮设计成圆形．
（3）若路面如图6形状，可看成由半径为2的一些等弧首尾连结而成，若

ˆ

EF

长为

π

9

，为确保车轮平稳滚动，则该车轮应设计成边数为几的正多边形？