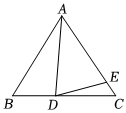
已知△ABC，AB=AC，D为BC上一点，E为AC上一点，AD=AE．
（1）如果∠BAD=20°，∠DAE=30°，那么∠EDC=
10
10
°；
（2）如果∠ABC=60°，∠ADE=80°，那么∠BAD=
40
40
°，∠CDE=
20
20
°；
（3）猜想∠BAD和∠CDE之间的关系式，并说明理由．

【答案】10；40；20

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/7/28 8:0:9组卷：20引用：1难度：0.7

相似题

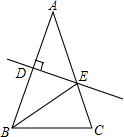1．等腰△ABC的周长为25，底边BC=7，AB的垂直平分线DE交AB于点D，交AC于点E，则△BEC的周长为

．
发布：2025/6/23 14:30:1组卷：47引用：2难度：0.9
解析
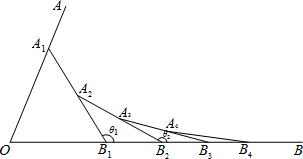
2．如图，已知∠AOB=α，在射线OA、OB上分别取点A₁、B₁，使OA₁=OB₁，连接A₁B₁，在B₁A₁、B₁B上分别取点A₂、B₂，使B₁B₂=B₁A₂，连接A₂B₂…按此规律下去，记∠A₂B₁B₂=θ₁，∠A₃B₂B₃=θ₂，…，∠A_n+1B_nB_n+1=θ_n，则θ₂₀₁₂-θ₂₀₁₁的值为（　　）
A．
180
°
-
α
2
2012
B．
180
°
+
α
2
2012
C．
180
°
-
α
2
2011
D．
180
°
+
α
2
2011
发布：2025/6/23 14:30:1组卷：92引用：3难度：0.7
解析
3．等腰三角形是

图形，其对称轴是

．
发布：2025/6/23 12:30:1组卷：62引用：7难度：0.5
解析

A． 180 ° - α 2 2012	B． 180 ° + α 2 2012
C． 180 ° - α 2 2011	D． 180 ° + α 2 2011

已知△ABC，AB=AC，D为BC上一点，E为AC上一点，AD=AE．（1）如果∠BAD=20°，∠DAE=30°，那么∠EDC=1010°；（2）如果∠ABC=60°，∠ADE=80°，那么∠BAD=4040°，∠CDE=2020°；（3）猜想∠BAD和∠CDE之间的关系式，并说明理由．