数学兴趣小组围绕“三角形的内角和是180°”，进行了一系列探究，过程如下：
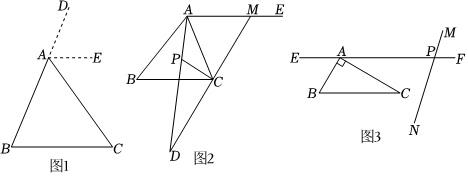
【论证】如图1，延长BA至D，过点A作AE∥BC，就可以说明∠BAC+∠B+∠C=180°成立，即：三角形的内角和为180°，请完成上述说理过程．
【应用】如图2，在△ABC中，∠BAC的平分线与∠ACB的角平分线交于点P，过点A作AE∥BC，M在射线AE上，且∠ACM=∠AMC，MC的延长线与AP的延长线交于点D．
①求∠DCP的度数；
②设∠B=α，请用α的代数式表示∠D．
【拓展】如图3，在△ABC中，∠BAC=90°，∠ACB=30°，过点A作EF∥BC，直线MN与EF相交于A点右侧的点P，∠APN=75°．△ABC绕点A以每秒12°的速度顺时针方向旋转，同时MN绕点P以每秒5°的速度顺时针方向旋转，与EF重合时MN再绕着点P以原速度逆时针方向旋转，当△ABC旋转一周时，运动全部停止，设运动时间为t秒，在旋转过程中，是否某一时刻，使得MN∥BC？若存在，求t的值；若不存在，请说明理由．