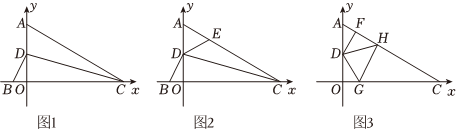
如图，点A、D在y轴正半轴上，点B、C在x轴上，CD平分∠ACB与y轴交于D点．
（1）如图1，∠CAO=∠DBO，求证：AC=BC；
（2）如图2，点C的坐标为（4，0），点E为AC上一点，且∠DEA=∠DBO，求BC+EC的长；
（3）如图3，过D作DF⊥AC于F点，点H为FC上一动点，点G为OC上一动点，当H在FC上移动，点G在OC上移动时，始终满足∠GDH=75°、∠FDO=150°，试判断FH、GH、OG这三者之间的数量关系，写出你的结论并加以证明．
【考点】三角形综合题．
【答案】（1）见解答；（2）8；（3）GH=OG+FH．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/9 14:0:8组卷：61引用：1难度：0.3
相似题
-
1．如图1：AC∥EF，AC=EF，AE=BD．
求证：△ABC≌△EDF．
如图2：DF=CE，AD=BC，∠D=∠C．
求证：△AED≌△BFC．
如图3：AB=AC，AD=AE，AB⊥AC，AD⊥AE．求证：（1）∠B=∠C，（2）BD=CE．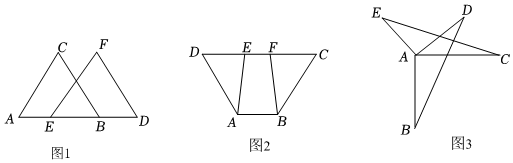
发布：2025/6/20 4:30:2组卷：11引用：1难度：0.4 -
2．如图，在等腰直角△ABC中，∠ACB=90°．点P在线段BC上，延长BC至点Q，使得CQ=CP，连接AP，AQ．过点B作BD⊥AQ于点D，交AP于点E，交AC于点F．K是线段AD上的一个动点（与点A，D不重合），过点K作GN⊥AP于点H，交AB于点G，交AC于点M，交FD的延长线于点N．
（1）依题意补全图1；
（2）求证：NM=NF；
（3）若AM=CP，用等式表示线段AE，GN与BN之间的数量关系，并证明．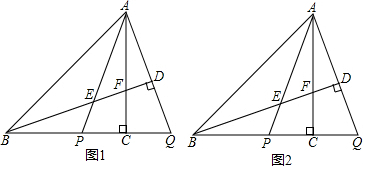
发布：2025/6/20 3:30:1组卷：1341引用：5难度：0.2 -
3．如图，在△ABC中，∠ACB=90°，∠ABC=30°，△CDE是等边三角形，点D在边AB上．
（1）如图1，当点E在边BC上时，求证DE=EB；
（2）如图2，当点E在△ABC内部时，猜想ED和EB数量关系，并加以证明；
（3）如图3，当点E在△ABC外部时，EH⊥AB于点H，过点E作GE∥AB，交线段AC的延长线于点G，AG=5CG，BH=3．求CG的长．发布：2025/6/20 8:30:2组卷：1957引用：13难度：0.1
