对于△ABC及其边上的一点P，给出如下定义：如果点M1，M2，M3…Mn都在△ABC的边上，且PM1=PM2=PM3=…=PMn，那么称点M1，M2，M3…Mn为△ABC关于点P的等距点，线段PM1，PM2，PM3…PMn为△ABC关于点P的等距线段．
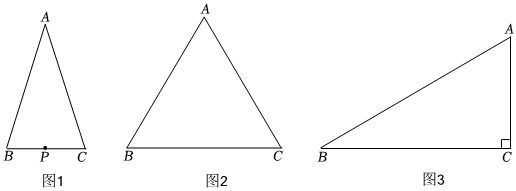
（1）如图1，△ABC中，∠A＜90°，AB=AC，点P是BC的中点．
①点B，C 是是△ABC关于点P的等距点，线段PA，PB 不是不是△ABC关于点P的等距线段；（填“是”或“不是”）
②△ABC关于点P的两个等距点M1，M2分别在边AB，AC上，当相应的等距线段最短时，在图1中画出线段PM1，PM2；
（2）如图2，△ABC是边长为4的等边三角形，点P在BC上，点C，D是△ABC关于点P的等距点，且PC=1，直接写出线段DC的长；
（3）如图3，在Rt△ABC中，∠C=90°，∠B=30°，点P在BC上，△ABC关于点P的等距点恰好有两个，且其中一个是点C，若BC=a,直接写出PC长的取值范围（用含a的式子表示）．
【考点】三角形综合题．
【答案】是；不是
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/9 8:0:9组卷：46引用：2难度：0.5
相似题
-
1．探索：如图①，以△ABC的边AB、AC为直角边，A为直角顶点，向外作等腰直角△ABD和等腰直角△ACE，连接BE、CD，试确定BE与CD有怎样数量关系，并说明理由．
应用：如图②，要测量池塘两岸B、E两地之间的距离，已知测得∠ABC=45°，∠CAE=90°，AB=BC=100米，AC=AE，求BE的长．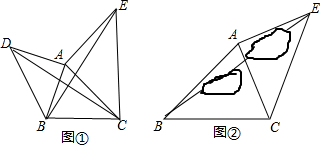
发布：2025/6/20 10:0:1组卷：1305引用：4难度：0.1 -
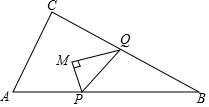2．如图，在△ABC中，∠ACB=90°，AC=3，BC=6．动点P从点A出发，沿AB以每秒个单位长度的速度向终点B匀速运动，同时点Q从点B出发，沿折线BC-CA以每秒3个单位长度的速度向终点A匀速运动．当点P不与点A、B重合时，连结PQ，以PQ为斜边作Rt△PMQ，使∠PMQ=90°，tan∠MPQ=5，且点M、B在直线PQ的两侧．设点Q的运动时间为t秒．43
（1）用含t的代数式表示CQ的长．
（2）当PM⊥AB时，求PQ的长．
（3）当点M在△ABC内部时，求t的取值范围．
（4）当△ABC的边与△PMO的边所夹的角被线段PQ平分时，直接写出t的值．发布：2025/6/20 10:30:1组卷：82引用：1难度：0.1 -
3．如图1，在△ABC中，BO⊥AC于点O，AO=BO=3，OC=1，过点A作AH⊥BC于点H，交BO于点P．
（1）求线段OP的长度；
（2）连接OH，求证：∠OHP=45°；
（3）如图2，若点D为AB的中点，点M为线段BO延长线上一动点，连接MD，过点D作DN⊥DM交线段OA延长线于N点，则S△BDM-S△ADN的值是否发生改变，如改变，求出该值的变化范围；若不改变，求该式子的值．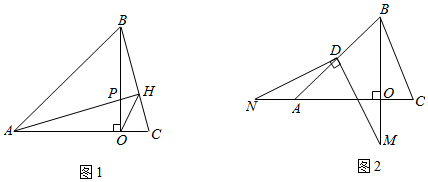
发布：2025/6/20 14:30:1组卷：3194引用：5难度：0.3
