定义：在平面直角坐标系xOy中，将点P（x,y）变换为P′（kx+b,by+k）（k,b为常数），我们把这种变换称为“R变换”．
（1）当k=0，b=2时，点P（1，2）经过“R变换”得到的点P′的坐标为 （2，4）（2，4）；
（2）已知点A（2，1），B（a-b,c+32a），C（6-2b,-c4-12）经过“R变换”的对应点分别是A′（4，3），B′（-2-2c,9-2b+c），C′．
①已知M（2m,3-2m），N（n-1，-2n-3）．MN⊥BC′且MN=2BC'，请求出MN两点的坐标；
②是否存在x轴上的点Q使得△A'B'C′的面积是△QBC面积的2倍，若存在，求出a的值，若不存在，说明理由．
3
2
c
4
1
2
【考点】三角形综合题．
【答案】（2，4）
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/15 8:0:9组卷：274引用：1难度：0.7
相似题
-
1．已知直角△ABC，∠BAC=90°，D是斜边BC的中点，E、F分别是AB、AC边上的点，且DE⊥DF，连接EF．
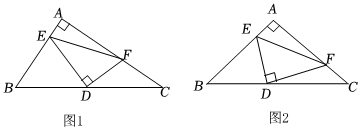
（1）如图1，求证：∠BED=∠AFD；
（2）如图1，求证：BE2+CF2=EF2；
（3）如图2，当∠ABC=45°，若BE=4，CF=3，求△DEF的面积．发布：2024/12/23 14:0:1组卷：216引用：3难度：0.2 -
2．已知A（0，4），B（-4，0），D（9，4），C（12，0），动点P从点A出发，在线段AD上，以每秒1个单位的速度向点D运动：动点Q从点C出发，在线段BC上，以每秒2个单位的速度向点B运动，点P、Q同时出发，当其中一个点到达终点时，另一个点随之停止运动，设运动时间为t（秒）．
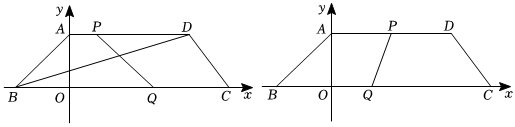
（1）当t=秒时，PQ平分线段BD；
（2）当t=秒时，PQ⊥x轴；
（3）当时，求t的值．∠PQC=12∠D发布：2024/12/23 15:0:1组卷：186引用：3难度：0.1 -
3．一副三角板如图1摆放，∠C=∠DFE=90°，∠B=30°，∠E=45°，点F在BC上，点A在DF上，且AF平分∠CAB，现将三角板DFE绕点F顺时针旋转（当点D落在射线FB上时停止旋转）．
（1）当∠AFD=°时，DF∥AC；当∠AFD=°时，DF⊥AB；
（2）在旋转过程中，DF与AB的交点记为P，如图2，若△AFP有两个内角相等，求∠APD的度数；
（3）当边DE与边AB、BC分别交于点M、N时，如图3，若∠AFM=2∠BMN，比较∠FMN与∠FNM的大小，并说明理由．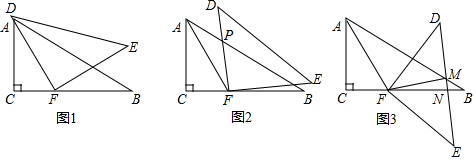
发布：2024/12/23 18:30:1组卷：1761引用：10难度：0.1
