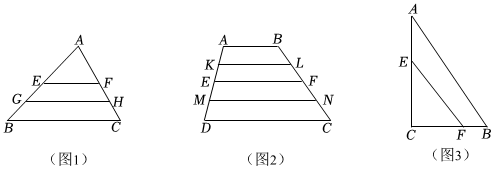
（一）感知：如图1，EF是△ABC的中位线，BC=a,G、H分别是BE、CF的中点，则GH=34a34a；（用字母a表示）GH与EF+BC间有怎样的相等关系：EF+BC=2GHEF+BC=2GH．
（二）探索：如图2，在四边形ABCD中，AB∥CD，其中AB=a,CD=b,（1）E是AD的中点，EF∥CD交BC于点F，则EF=12（a+b）12（a+b）.（用字母a,b表示）
（2）K在AD上，L在BC上，KL∥CD，且使四边形ABLK∽四边形KLCD，则KL=abab.（用字母a,b表示）
（3）M在AD上，N在BC上，MN∥CD，且MN平分四边形ABCD的面积，求MN的长．（用字母a,b表示）
（三）猜想：KL、EF、MN间的大小关系：ab≤12（a+b）≤a2+b22ab≤12（a+b）≤a2+b22，（用a、b的表达式表示）并对EF与MN间的关系进行证明；
（四）应用：如图3，在Rt△ABC中，∠C=90°，BC=3，AC=4，点E、F分别在AC、BC上，EF平分△ABC的面积，求△CEF周长的最小值．
3
4
3
4
1
2
1
2
ab
ab
ab
≤
1
2
（
a
+
b
）
≤
a
2
+
b
2
2
ab
≤
1
2
（
a
+
b
）
≤
a
2
+
b
2
2
【考点】相似形综合题．
【答案】a；EF+BC=2GH；（a+b）；；
3
4
1
2
ab
ab
≤
1
2
（
a
+
b
）
≤
a
2
+
b
2
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/14 8:0:9组卷：151引用：1难度：0.2
相似题
-
1．问题提出
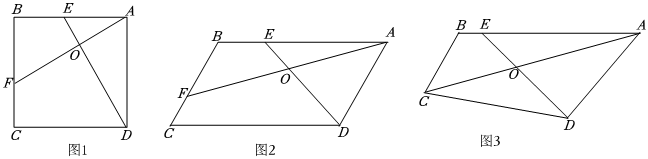
（1）如图1，正方形ABCD，点E、F分别在边AB、BC上，连接AF与DE交于点O，有∠FOD=90°，则=；AFDE
（2）如图2，平行四边形ABCD，AB=，BC=285，点E、F分别在边AB、BC上，连接AF与DE交于点O，当∠FOD=∠B时，你能求出165的比值吗？请写出求比值的过程；AFDE
问题解决
（3）如图3，四边形ABCD，AB=113，∠B=∠ADC=120°，BC=45，，点E在边AB上，连接AC与DE交于点O，当∠COD=∠B时，求CDAD=97的值．ACDE发布：2025/5/23 8:30:2组卷：2509引用：4难度：0.1 -
2．如图1，正方形AFEG与正方形ABCD有公共点A，点G，F分别在AD，AB上，点E在正方形ABCD的对角线AC上．将正方形AFEG绕A点逆时针方向旋转，旋转角为α（0°≤α≤360°）．
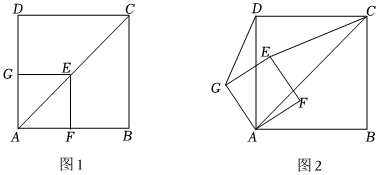
（1）当α=0°时，= ；CEDG
（2）如图2，当0°＜α＜45°时，连接CE，DG，是否为定值？请说明理由；CEDG
（3）若，AG=2，当C，G，E三点共线时，求DG的长度．AB=22发布：2025/5/23 8:30:2组卷：455引用：2难度：0.3 -
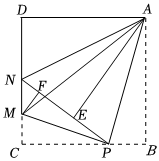3．如图，在边长为2的正方形ABCD中，P是BC边上一动点（不含B，C两点），将△ABP沿直线AP翻折，点B落在点E处，在CD上有一点M，使得将△CMP沿直线MP翻折后，点C落在直线PE上的点F处，直线PE交CD于点N，连接MA，NA．
（1）求证：△CMP∽△BPA；
（2）求△CNP的周长；
（3）求线段AM长度的最小值．发布：2025/5/23 8:30:2组卷：168引用：2难度：0.2
