如图，已知AM∥DN，∠A=60°，点P是射线AM上一动点（与点A不重合），BC，BD分别平分∠ABP和∠PBN分别交射线AM于点C，D．
（1）求∠ABN、∠CBD的度数．
（2）当点P运动时，∠APB与∠ADB之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由；若变化，请写出变化规律．
（3）当点P运动到使∠ACB=∠ABD时，直接写出∠ABC的度数．
【考点】平行线的性质．
【答案】（1）∠ABN=120°，∠CBD=60°；
（2）∠APB=2∠ADB；
（3）30°．
（2）∠APB=2∠ADB；
（3）30°．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/21 8:0:9组卷：73引用：3难度：0.5
相似题
-
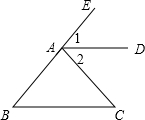1．如图，AD平分∠EAC，AD∥BC，试探索∠B与∠C的数量关系，写出你的结论并说明理由．发布：2025/6/7 17:30:1组卷：81引用：3难度：0.7 -
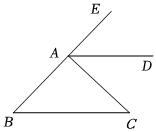2．如图，已知AD∥BC，∠B=40o，AD平分∠EAC，求∠EAD与∠C的度数．发布：2025/6/7 17:0:1组卷：71引用：1难度：0.6 -
3．①如图1，AB∥CD，则∠A+∠E+∠C=360°；
②如图2，AB∥CD，则∠P=∠A-∠C；
③如图3，AB∥CD，则∠E=∠A+∠1；
④如图4，直线AB∥CD∥EF，点O在直线EF上，则∠α-∠β+∠γ=180°．
以上结论正确的个数是（ ）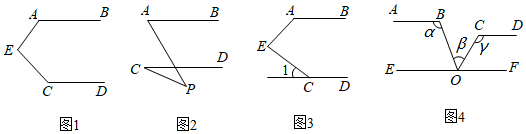
发布：2025/6/7 17:0:1组卷：215引用：6难度：0.6
