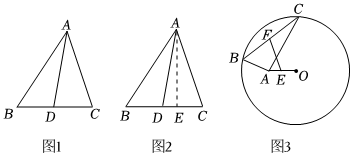
阅读理解：小明热爱数学，在课外书上看到了一个有趣的定理——“中线长定理”：三角形两边的平方和等于第三边的一半与第三边上的中线的平方和的两倍．如图1，在△ABC中，点D为BC的中点，根据“中线长定理”，可得：AB2+AC2=2AD2+2BD2．
小明尝试对它进行证明，部分过程如下：
解：过点A作AE⊥BC于点E，如图2，在Rt△ABE中，AB2=AE2+BE2，
同理可得：AC2=AE2+CE2，AD2=AE2+DE2，
为证明的方便，不妨设BD=CD=x,DE=y,
∴AB2+AC2=AE2+BE2+AE2+CE2=…
（1）请你完成小明剩余的证明过程；
（2）在△ABC中，点D为BC的中点，AB=6，AC=4，BC=8，求AD的长；
（3）如图3，⊙O的半径为6，点A在圆内，且OA=22，点B和点C在⊙O上，且∠BAC=90°，点E、F分别为AO、BC的中点，求EF的长．
OA
=
2
2
【考点】圆的综合题．
【答案】（1）见解答过程；
（2）；
（3）4．
（2）
10
（3）4．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/29 10:0:1组卷：89引用：1难度：0.3
相似题
-
1．已知，线段AB是⊙O的直径，弦CD⊥AB于点H，点M是优弧CBD上的任意一点，AH=2，CH=4．
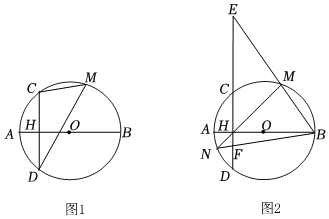
（1）如图1，
①求⊙O的半径；
②求sin∠CMD的值．
（2）如图2，直线BM交直线CD于点E，直线MH交⊙O于点N，连结BN交CD于点F，求HE•FH的值．发布：2025/6/7 7:0:1组卷：476引用：2难度：0.3 -
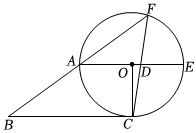2．如图，四边形OABC中，AO∥BC，∠AOC=90°，AO=3，AB=5．以O为圆心，OA为半径作圆，⊙O经过点C，且与BA的延长线交于F．延长AO交圆于E，连接FC交AE于点D．
（1）求证：BC是⊙O的切线；
（2）求cos∠FAE的值；
（3）求线段OD的长．发布：2025/6/7 5:0:1组卷：79引用：1难度：0.3 -
3．等腰三角形AFG中AF=AG，且内接于圆O，D、E为边FG上两点（D在F、E之间），分别延长AD、AE交圆O于B、C两点（如图1），记∠BAF=α，∠AFG=β．
（1）求∠ACB的大小（用α，β表示）；
（2）连接CF，交AB于H（如图2）．若β=45°，且BC×EF=AE×CF．求证：∠AHC=2∠BAC；
（3）在（2）的条件下，取CH中点M，连接OM、GM（如图3），若∠OGM=2α-45°，
①求证：GM∥BC，GM=BC；12
②请直接写出的值．OMMC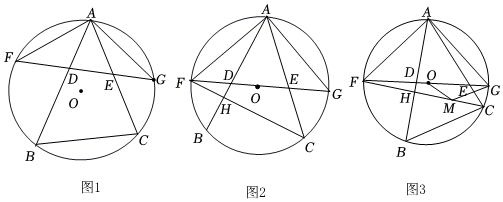
发布：2025/6/7 16:0:2组卷：1490引用：8难度：0.1
