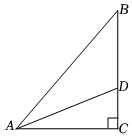
初二（8）班“数学兴趣小组”在学习“勾股定理”章节的内容后，遇到这样的问题．如图在直角三角形ABC中，CA=6，CB=8．点D是边CB上的一个动点（不与B、C重合）连接AD．若△ADB是等腰三角形，求线段CD的长．
方法一：王朗坤同学利用学习的勾股定理进行解决，当△ABD为等腰三角形时，AD=BD，设CD=x,则BD=8-x,所以AD=BD=8-x.在直角三角形ACD中，利用勾股定理，可得：62+x2=（8-x）2．
解得：x=74．所以当△ABD为等腰三角形时，CD的长为74．
方法二：王子贺同学提前预习了函数这一章节的内容，他尝试利用函数的方法探究并解决该问题．
下面是他的探究过程，请你补充完整．
（1）根据点D在边BC上的不同位置，画出相应图形，测量出线段CD、AD的长度，得出下面的表格：
7
4
7
4
| CD | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| AD | 6 | 6.1 | 6.3 | 6.7 | 7.2 | 7.8 | 8.5 | 9.2 | a |
10
10
．②王子贺同学分析得知可以不用测量BD的值，因为CD与BD满足关系式
CD+BD=8
CD+BD=8
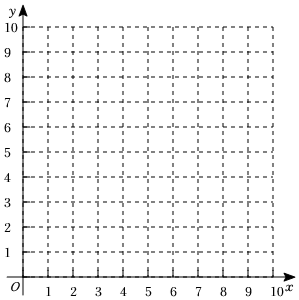
；（2）将CD的长作为自变量x,AD的长为x的函数，记为y,在下面平面直角坐标系中画出函数y关于x的图象，并写出该函数的一条性质：
y随x的增大而增大
y随x的增大而增大
．（3）继续在平面直角坐标系画出BD（BD用y1表示）关于CD的函数图象，并结合图形直接写出，当△ABD为等腰三角形时，线段CD的长度的近似值（精确到0.1）．
【考点】三角形综合题．
【答案】10；CD+BD=8；y随x的增大而增大
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/29 8:0:10组卷：106引用：3难度：0.3
相似题
-
1．已知△ABC为等腰三角形，AB=AC，点D为直线BC上一动点（点D不与点B、点C重合）．以AD为边作△ADE，且AD=AE，连接CE，∠BAC=∠DAE．
（1）如图1，当点D在边BC上时，试说明：①△ABD≌△ACE；②BC=DC+CE；
（2）如图2，当点D在边BC的延长线上时，其他条件不变，探究线段BC、DC、CE之间存在的数量关系，并说明理由．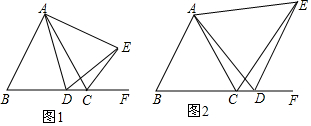
发布：2025/5/24 7:0:1组卷：805引用：5难度：0.4 -
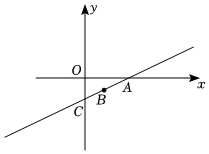2．如图，在平面直角坐标系中，点A坐标为（6，0），点B坐标为（2，-2），直线AB与y轴交于点C，点B关于y轴的对称点为点D．
（1）请直接写出点D的坐标为 ；
（2）在直线BD上找一点E，使△ACE是直角三角形，请直接写出点E的横坐标为 ．发布：2025/5/24 7:0:1组卷：45引用：1难度：0.2 -
3．如图，在△ABC中，∠BAC=90°，AB=AC=12，点P在边AB上，D、E分别为BC、PC的中点，连接DE．过点E作BC的垂线，与BC、AC分别交于F、G两点．连接DG，交PC于点H．
（1）∠EDC的度数为 °；
（2）连接PG，求△APG的面积的最大值；
（3）PE与DG存在怎样的位置关系与数量关系？请说明理由；
（4）求的最大值．CHCE发布：2025/5/24 8:30:1组卷：3141引用：4难度：0.1
