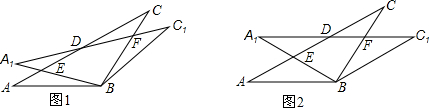
在△ABC中，AB=BC=2，∠ABC=120°，将△ABC绕点B顺时针旋转角α（0°＜α＜90°）得△A1BC1，A1B交AC于点E，A1C1分别交AC、BC于D、F两点．
（1）如图1，观察并猜想，在旋转过程中，线段BE与BF有怎样的数量关系？并证明你的结论；
（2）如图2，当α=30°时，试判断四边形BC1DA的形状，并说明理由．
【考点】旋转的性质．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/27 2:0:8组卷：1608引用：17难度：0.3
相似题
-
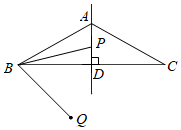1．如图，在△ABC中，∠BAC=120°，AB=AC=3，AD⊥BC，点P为直线AD上一点，连接BP，将BP绕点B顺时针旋转60°得到BQ，则点A、Q距离的最小值为．发布：2025/5/25 0:30:1组卷：818引用：2难度：0.6 -
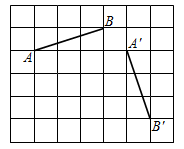2．如图，在正方形网格中，线段AB绕某点顺时针旋转角α（0＜α＜180）得到线段A'B'，点A与点A'是对应点，点B与点B'是对应点，则α等于 ．发布：2025/5/25 0:30:1组卷：215引用：4难度：0.7 -
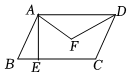3．如图，在▱ABCD中，AB=6，BC=10，∠B=60°，点E在线段BC上运动（含B、C两点）．连接AE，以点A为中心，将线段AE逆时针旋转60°得到AF，连接DF，则线段DF长度的最小值为 ．发布：2025/5/25 0:30:1组卷：730引用：6难度：0.4
