【情境建模】（1）苏科版教材八年级上册第60页，研究了等腰三角形的轴对称性，我们知道“等腰三角形底边上的高线、中线和顶角平分线重合”，简称“三线合一”．
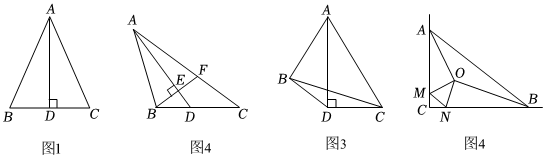
小明尝试着逆向思考：若三角形一个角的平分线与这个角对边上的高重合，则这个三角形是等腰三角形．如图1，已知，点D在△ABC的边BC上，AD平分∠BAC，且AD⊥BC，求证：AB=AC．请你帮助小明完成证明．
请尝试直接应用“情境建模”中小明反思出的结论解决下列问题：
【理解内化】（2）①如图2，在△ABC中，AD是角平分线，过点B作AD的垂线交AD、AC于点E、F，∠ABF=2∠C，求证：BE=12（AC-AB）．
②如图3，在四边形ABDC中，BC=7，AC-AB=2，AD平分∠CAB，AD⊥CD，当△BCD的面积最大时，请直接写出此时CD的长．
【拓展应用】（3）如图4，△ABC是两条公路岔路口绿化施工的一块区域示意图，其中∠ACB=90°，AC=15m,BC=20m,该绿化带中修建了健身步道．OA、OB、OM、ON、MN，其中入口M、N分别在AC、BC上，步道OA、OB分别平分∠BAC和∠ABC，OM⊥OA，ON⊥OB．现要用围挡完全封闭△CMN区域，修建地下排水和地上公益广告等设施，请直接写出围挡的长度．（步道宽度和接头忽略不计）
BE
=
1
2
（
AC
-
AB
）
BC
=
7
AC
-
AB
=
2
【考点】四边形综合题．
【答案】（1）证明见解析；
（2）①证明见解析；
②；
（3）10m．
（2）①证明见解析；
②
3
2
（3）10m．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/12 2:0:2组卷：344引用：1难度：0.5
相似题
-
1．已知，正方形ABCD中，∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交CB，DC（或它们的延长线）于点M，N，AH⊥MN于点H．
（1）如图①，当∠MAN绕点A旋转到BM=DN时，请你直接写出AH与AB的数量关系：．
（2）如图②，当∠MAN绕点A旋转到BM≠DN时，（1）中发现的AH与AB的数量关系还成立吗？如果不成立请写出理由，如果成立请证明；
（3）如图③，已知∠MAN=45°，AH⊥MN于点H，且MH=2，NH=3，探求AH满足的数量关系．（可利用（2）得到的结论）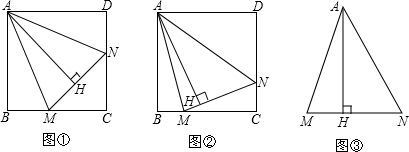
发布：2025/6/17 11:30:1组卷：878引用：1难度：0.3 -
2．请问读下列材料，并解答相应的问题
在Rt△ABC中、如果锐角A确定，那么角A的对边与邻边的比值随之确定，这个比叫做角A的正切，记作tanA，这是我们熟悉的三角函数中关于正切的定义．你不知道的是，世界上最早的正切函数表是由我国唐代一位叫做僧一行（683-727）的僧人在其所著《大衍历》中首次创作的．他通过某地影长的观测，求人阳天顶距进而求出该地各节气初日影长的方法，并为此编制了0度到80度的正切函数表．
我们摘取了部分正切函数表，如图所示，当角的度数是63.2度时，我们查表可知其对应的正切值为1.97，反之，如果已知一个角的正切值1.97，则这个角的度数是63.2度．
现已知矩形ABCD中，AD=4、AB=8，AC是对角线，点E是线段AB上的动点（点E不与A、B重合），点P是线段AC上的动点，（点P不与A、C重合）∠DPE=90°．角度 正切值 63.2 1.97 63.3 1.98 63.4 1.99 63.5 2.00 63.6 2.01 63.7 2.02
①若AE=AD，∠DPE=90°，测得∠DEP=63.5°，则查表可知tan∠DEP=，此时可求出线段PE=．（直接写出答案）
②若AE=3，∠DPE=90°，若此时点P恰好是AC中点，请直接写出tan∠DEP=．
③若AE的值不是3，那么在变化过程中，tan∠DEP是否发生变化？请说明理由．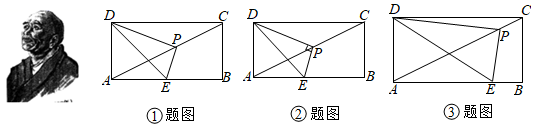
发布：2025/6/17 10:0:1组卷：58引用：1难度：0.4 -
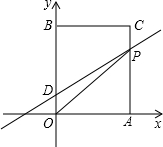3．如图在平面直角坐标系中，O是坐标原点，矩形OACB的顶点A，B分别在x轴、y轴上，已知OA=3，点D为y轴上一点，其坐标为（0，1），若连接CD，则CD=5，点P从点A出发以每秒1个单位的速度沿线段A-C-B的方向运动，当点P与点B重合时停止运动，运动时间为t秒
（1）求B，C两点坐标；
（2）求△OPD的面积S关于t的函数关系式；
（3）当点D关于OP的对称点E落在x轴上时，请直接写出点E的坐标，并求出此时的t值．发布：2025/6/17 10:30:2组卷：135引用：3难度：0.1
