【阅读理解】
我们在分析解决某些数学问题时，经常要比较两个数或代数式的大小，解决问题的策略一般都是进行一定的转化，其中“作差法”就是常用的方法之一．作差法：就是通过作差、变形，利用差的符号确定它们的大小，即要比较代数式A、B的大小，只要算A-B的值，若A-B＞0，则A＞B；若A-B=0，则A=B；若A-B＜0，则A＜B．
【知识运用】
（1）请用上述方法比较下列代数式的大小（用“＞、=、＜”填空）：
①x-1

＞

＞

x+3；
②若a＜b＜0，则a²

＞

＞

b²；
（2）试比较与6x²+2x+1与5x²+4x-3的大小，并说明理由；
【类比运用】
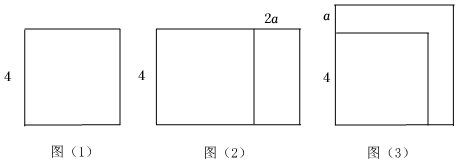
（3）图（1）是边长为4的正方形，将正方形一组对边保持不变，另一组对边增加2a（a＞0）得到如图（2）所示的长方形，此长方形的面积为S₁；将正方形的边长增加a,得到如图（3）所示的大正方形，此正方形的面积为S₂；则S₁与S₂的大小关系为：S₁

＜

＜

S₂；
（4）已知M=2020×2023，N=2021×2022，试运用上述方法比较M、N的大小，并说明理由．