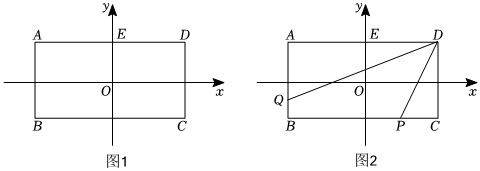
如图1，以长方形ABCD的中心O为原点，平行于BC的直线为x轴建立平面直角坐标系，已知点A（-b,a），B（-b,-a），C（b,-a），D（b,a），且满足（a-3）2+b-6=0．
（1）直接写出：a=33，b=66；
（2）设AD的中点为E，点M是y轴上的点，且△CME的面积是长方形ABCD面积的16，求点M的坐标；
（3）如图2，若点P从C点出发沿CB方向匀速移动（不超过点B），运动速度为2个单位/秒，同时点Q从B点出发沿BA方向匀速移动（不超过点A），运动速度为1个单位/秒，设移动时间为t秒．
①CP=2t2t，AQ=6-t6-t（用含t的式子表示）；
②在点P，Q移动过程中，当△ADQ的面积是△DCP的面积的一半时，求出P、Q两点的坐标；
③在点P、Q移动过程中，四边形PBQD的面积是否发生变化？若不变，求其值；若变化，求其变化范围．
b
-
6
1
6
【考点】四边形综合题．
【答案】3；6；2t；6-t
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/23 8:0:10组卷：60引用：1难度：0.5
相似题
-
1．如图，△ABC中，∠CAB与∠CBA均为锐角，分别以CA、CB为边向△ABC外侧作正方形CADE和正方形CBFG，再作DD1⊥直线AB于D1，FF1⊥直线AB于F1．
（1）如图（1），过点C作CH⊥AB于H，求证：DD1+FF1=AB；
（2）如图（2），连接EG，问△ABC的面积与△ECG的面积是否相等？请说明理由；
（3）如图（3），过点C作CM⊥EG于M，延长MC交AB于点N，求证：AN=BN．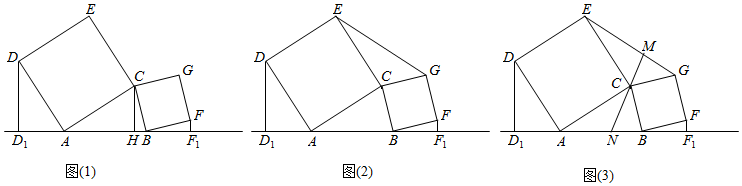
发布：2025/6/21 3:30:1组卷：127引用：3难度：0.5 -
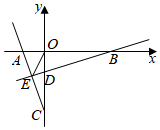2．在平面直角坐标系中，已知点A（a,0），C（0，b）且a,b满足（a+1）2+=0．b+3
（1）直接写出：a=，b=；
（2）点B在x轴正半轴上，过点B作BE⊥AC于点E，交y轴于点D（0，-1），连接OE，若OE平分∠AEB，求点B和点E的坐标；
（3）在（2）的条件下，若点P是直线BE上的动点，点Q是该平面内某一点，且以点P、Q、A、B为顶点的四边形是菱形，直接写出点P的坐标．发布：2025/6/21 13:30:2组卷：105引用：1难度：0.3 -
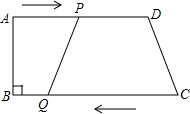3．如图，在梯形ABCD中，AD∥BC，∠B=90°，AB=10cm,AD=20cm,BC=24cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动，动点Q从点C开始沿CB方向向点B以3cm/s的速度运动．P、Q两点同时出发，设运动时间为t,当其中一点到达端点时，另一点随之停止运动．
（1）当t=3时，PD=，CQ=．
（2）当t为何值时，四边形CDPQ是平行四边形？请说明理由．
（3）在运动过程中，设四边形CDPQ的面积为S，写出S与t的函数关系式，并求当t为何值时，S的值最大，最大值是多少？发布：2025/6/21 2:0:1组卷：147引用：2难度：0.3
