如何通过代数推理证明反比例函数图象的性质?
代数推理指从一定条件出发,依据代数的定义、公式、运算法则、等式的性质、不等式的性质等证明已知结果或结论.
我们不妨来试试
(1)性质:反比例函数y=3x的图象是中心对称图形,对称中心是原点.
证:在函数上任取一点A(x,3x),
则点A关于原点对称的点B为( -x-x,-3x-3x),
∵(-x)•(-3x)=3(-x)•(-3x)=3,
∴点B也在反比例函数y=3x的图象上,
∵点A是反比例函数y=3x上的任意一点,它关于原点对称的点都在反比例函数y=3x的图象上,
∴反比例函数y=3x的图象是中心对称图形,对称中心是原点.
仿照上述方法,尝试证明
(2)性质:反比例函数y=3x的图象关于直线y=x对称,关于直线y=-x对称.
运用代数推理进行证明
(3)证明:对于反比例函数y=3x,当x>0时,y随x的增大而减小.
3
x
3
x
3
x
3
x
3
x
3
x
3
x
3
x
3
x
3
x
3
x
3
x
【答案】-x;-;(-x)•(-)=3
3
x
3
x
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/6/7 8:0:9组卷:769引用:2难度:0.6
相似题
-
1.反比例函数y=
图象上有三个点(-2,y1),(-1,y2),(1,y3),则y1、y2、y3的大小关系是( )k2+1x发布:2024/12/23 16:30:2组卷:41引用:3难度:0.6 -
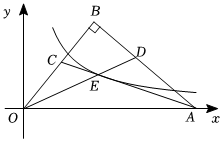 2.如图,在Rt△OAB中,∠OBA=90°,OA在x轴上,AC平分∠OAB,OD平分∠AOB,AC与OD相交于点E,且OC=,CE=5,反比例函数2的图象经过点E,则k的值为 .y=kx(k≠0,x>0)发布:2024/12/23 19:0:2组卷:1710引用:6难度:0.5
2.如图,在Rt△OAB中,∠OBA=90°,OA在x轴上,AC平分∠OAB,OD平分∠AOB,AC与OD相交于点E,且OC=,CE=5,反比例函数2的图象经过点E,则k的值为 .y=kx(k≠0,x>0)发布:2024/12/23 19:0:2组卷:1710引用:6难度:0.5 -
3.已知点(-1,y1),(2,y2),(3,y3)在反比例函数y=-
图象上,则y1,y2,y3之间的大小关系是( )6x发布:2024/12/23 16:30:2组卷:51引用:4难度:0.7


