下面是某数学兴趣小组探究问题的片段，请仔细阅读，并完成任务．
【问题提出】
如图1，在Rt△ABC中，∠ACB=90°，AC=BC，点D在AB上，请用尺规作图：在Rt△ABC外侧，以BC为边作△CBE≌△CAD．
【问题探究】
小明：如图2，分别以B、C为圆心，以AD、CD为半径画弧，两弧交于点E，连接BE、CE．则△CBE即为所求作的三角形．
小亮：如图3，过点B作BM⊥AB于点B，过点C作CN⊥DC于点C，BM、CN相交于点E，则△CBE即为所求作的三角形．
（1）小明得出△CBE≌△CAD的依据是 ①①，小亮得出△CBE≌△CAD的依据是 ③③．（横线上填序号：①SSS；②SAS；③ASA；④AAS）
【问题再探】
（2）在（1）中△CBE≌△CAD的条件下，连接AE．兴趣小组的同学们用几何画板测量发现△CAE和△CDB的面积相等．为了证明这个发现，A组同学会试延长线段AC至F点，使CF=CA，连接EF，从而得以证明（如图4）；B组同学过点D作DM⊥BC于点M，过点E作EN⊥AC于点N，从而得以证明（如图5），请你选取A组或B组中的一种方法完成证明过程．
【问题解决】
（3）如图6，已知∠ABM=∠ACB=90°，AC=BC，点D在AB上，BC=42，∠BCD=15°，若在射线BM上存在点E，使S△ACE=S△BCD，请求出相应的BE的长．
BC
=
4
2
【考点】三角形综合题．
【答案】①；③
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/3 8:0:9组卷：169引用：2难度：0.4
相似题
-
1．已知等腰三角形ABC，∠F=2∠ABC，CD=kBD，∠FGC=α．
（1）如图1，当k=1时，
①探究DG与CE之间的数量关系；
②探究BE，CG与CE之间的关系（用含α的式子表示）．
（2）如图2，当k≠1时，探究BE，CG与CE之间的数量关系（用含k,α的式子表示）．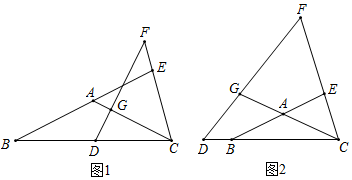
发布：2025/5/24 11:30:1组卷：343引用：3难度：0.2 -
2．已知：在△ABC中，AB=AC=10，BC=16，点P、D分别在射线CB、射线AC上，且满足∠APD=∠ABC．
（1）当点P在线段BC上时，如图1．
①如果CD=4.8，求BP的长；
②设B、P两点的距离为x,AP=y,求y关于x的函数关系式，并写出定义域．
（2）当BP=1时，求△CPD的面积．（直接写出结论，不必给出求解过程）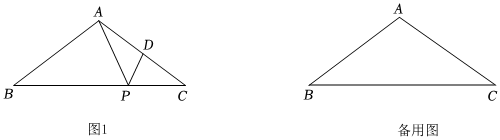
发布：2025/5/24 12:0:1组卷：310引用：1难度：0.1 -
3．如图，在△ABC中，∠A=α（0°＜α≤90°），将BC边绕点C逆时针旋转（180°-α）得到线段CD．
（1）判断∠B与∠ACD的数量关系并证明；
（2）将AC边绕点C顺时针旋转α得到线段CE，连接DE与AC边交于点M（不与点A，C重合）．
①用等式表示线段DM，EM之间的数量关系，并证明；
②若AB=a,AC=b,直接写出AM的长．（用含a,b的式子表示）发布：2025/5/24 14:0:2组卷：1301引用：9难度：0.2
