综合与实践：
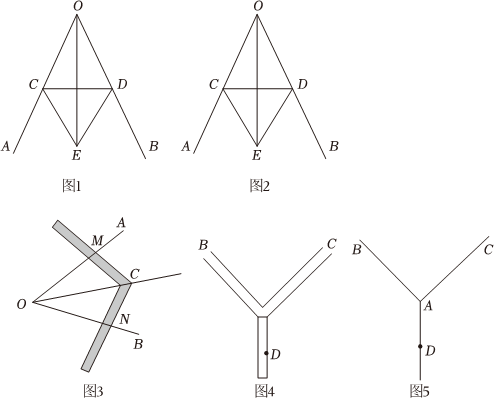
问题探究：（1）如图1是古希腊数学家欧几里得所著的《几何原本》第1卷命题9“平分一个已知角，”即：作一个已知角的平分线，如图2是欧几里得在《几何原本》中给出的角平分线作图法：在OA和OB上分别取点C和D，使得OC=OD，连接CD，以CD为边作等边三角形CDE，则OE就是∠AOB的平分线．请写出OE平分∠AOB的依据：SSSSSS；
类比迁移：（2）小明根据以上信息研究发现：△CDE不一定必须是等边三角形，只需CE=DE即可，他查阅资料；我国古代已经用角尺平分任意角，做法如下：如图3，在∠AOB的边OA，OB上分别取OM=ON，移动角尺，使角尺两边相同刻度分别与点M，N重合，则过角尺顶点C的射线OC是∠AOB的平分线，请说明此做法的理由；
拓展实践：（3）小明将研究应用于实践．如图4，校园的两条小路AB和AC，汇聚形成了一个岔路口A，现在学校要在两条小路之间安装一盏路灯E，使得路灯照亮两条小路（两条小路一样亮），并且路灯E到岔路口A的距离和休息椅D到岔路口A的距离相等，试问路灯应该安装在哪个位置？请用不带刻度的直尺和圆规在对应的示意图5中作出路灯E的位置．（保留作图痕迹，不写作法）
【考点】三角形综合题．
【答案】SSS
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/22 8:0:8组卷：1089引用：9难度：0.3
相似题
-
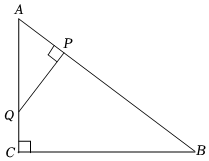1．如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，动点P从点A出发沿线段AB以每秒3个单位长的速度运动至点B，过点P作PQ⊥AB交射线AC于点Q，设点P的运动时间为t秒（t＞0）．
（1）线段AQ的长为 ，线段PQ的长为 .（用含t的代数式表示）
（2）当△APQ与△ABC的周长的比为1：4时，求t的值．
（3）设△APQ与△ABC重叠部分图形的面积为S，求S与t之间的函数关系式．发布：2025/6/25 4:0:1组卷：19引用：1难度：0.3 -
2．如图，在△ABC中，BC=5，AD⊥BC，BE⊥AC，AD，BE相交于点O，BD：CD=2：3，且AE=BE．
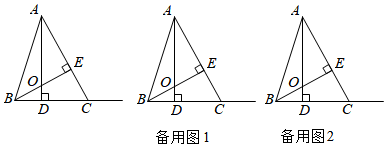
（1）求线段AO的长；
（2）动点P从点O出发，沿线段OA以每秒1个单位长度的速度向终点A运动，动点Q从点B出发沿射线BC以每秒4个单位长度的速度运动．P，Q两点同时出发，当点P到达A点时，P，Q两点同时停止运动．设点P的运动时间为t秒，△AOQ的面积为S，请用含t的式子表示S，并直接写出相应的t的取值范围；
（3）在（2）的条件下，点F是直线AC上的一点，且CF=BO，是否存在t值，使以点B，O，P为顶点的三角形与以点F，C，Q为顶点的三角形全等？若存在，请直接写出符合条件的t值；若不存在，请说明理由．发布：2025/6/25 5:0:1组卷：191引用：3难度：0.4 -
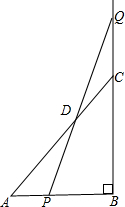3．已知等腰直角△ABC的直角边AB=BC=10cm,点P，Q分别从A．C两点同时出发，均以1cm/s的相同速度做直线运动，已知P沿射线AB运动，Q沿边BC的延长线运动，PQ与直线AC相交于点D．设P点运动时间为t,△PCQ的面积为S．
（1）求出S关于t的函数关系式．
（2）当点P在线段AB上时，点P运动几秒时，S△PCQ=S△ABC？14
（3）作PE⊥AC于点E，当点P．Q运动时，线段DE的长度是否改变？证明你的结论．发布：2025/6/23 23:0:10组卷：243引用：1难度：0.1
