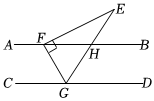
如图，已知AB∥CD，△EFG的顶点F、G分别落在直线AB、CD上，GE交AB于点H，GE平分∠FGD，如果∠EFG=90°，∠E=35°，求∠EFB的度数．
解：因为∠E+∠EFG+∠FGE=180°（

三角形内角和定理

三角形内角和定理

），
又因为∠EFG=90°，∠E=35°（已知），
所以∠FGE=

55

55

°．
因为GE平分∠FGD（已知），
所以∠FGE=∠

DGE

DGE

（角平分线的意义）．
因为AB∥CD（已知），
所以∠

EHB

EHB

=∠EGD（两直线平行，同位角相等）．
所以∠EHB=∠FGE（等量代换）．
所以∠EHB=55°．
因为∠EHB=∠EFB+∠

E

E

（三角形的一个外角等于与它不相邻的两个内角的和），
又因为∠E=35°（已知），
所以∠EFB=

20

20

°．