百钱买百鸡问题是记载于中国古代5—6世纪成书的《张邱建算经》中的一道不定方程组问题，其重要之处在于开创“一问多答”的先例，这是过去中国古算书中所没有的。其问题是这样的：今有鸡翁一，值钱伍；鸡母一，值钱三；鸡雏三，值钱一。凡百钱买鸡百只，问鸡翁、母、雏各几何？
用伪代码描述解决不定方程组5i+3j+k/3=100 i+j+k=100
的正整数解的算法如下：
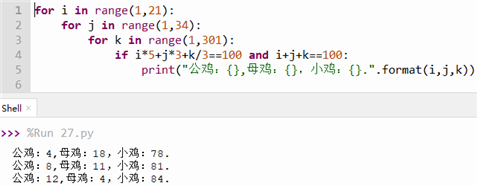
（1）该算法采用的是 穷举法/枚举法穷举法/枚举法（选填“穷举法”、“解析法”、“枚举法”、“分治法”）。
（2）该算法中，条件i*5+j*3+k/3==100 and i+j+k==100共被判断了多少次？（可以直接填计算结果也可以填计算式子）。
5 i + 3 j + k / 3 = 100 |
i + j + k = 100 |
【考点】枚举算法及程序实现．
【答案】穷举法/枚举法
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/27 10:35:59组卷：5引用：1难度：0.3
相似题
-
1．以下问题，适合用枚举法解决的是（ ）
发布：2024/11/8 11:30:1组卷：2引用：1难度：0.8 -
2．如果一个4位数恰好等于它的各位数字的4次方和，则这个数被称为“玫瑰花”数。例如1634就是一个玫瑰花数：1634=14+64+34+44。如果要求出所有的玫瑰花数，下列算法合适的是（ ）
发布：2024/11/16 22:30:5组卷：7引用：2难度：0.5 -
3．若一个三位数abc,满足abc=a3+b3+c3，则称abc为水仙花数。如三位数153满足13+53+33=1+125+27=153，则153是水仙花数。请把所有满足条件的水仙花数输出。
（1）分析问题。由题意可知，三位数的范围是100～999，我们可以让计算机一一检查每一个三位数，输出其中的水仙花数。设百位数字、十位数字、个位数字分别是a,b,c（0＜a≤9，0≤b≤9，0≤c≤9），这个三位数就可以表示为100×a+10×b+c,如果它正好等于各位数字的立方和，那么它就是水仙花数。
（2）设计算法。
①令a从1～9穷举；
②令b从0～9穷举；
③令c从0～9穷举；
④如果100×a+10×b+c和a3+b3+c3相等，那么就把它输出。
⑤转步骤③，重复执行③④⑤，直到c穷举完毕；
⑥转步骤②，重复执行②③④⑤⑥，直到b穷举完毕；
⑦转步骤①，重复执行①②③④⑤⑥⑦，直到a穷举完毕；
⑧跳出循环，结束。
（3）编写程序。
（4）调试程序。发布：2024/8/7 8:0:9组卷：1引用：0难度：0.4
