已知：在正方形ABCD中，动点P在对角线DB所在的直线上，以PC为直角边作等腰直角三角形PCQ，其中∠PCQ=90°，探究并解决下列问题：
（1）如图①，若点P在线段DB上，且AB=2．若连接BQ，请猜想：则BQ与DB的位置关系为 BO⊥DBBO⊥DB；PD2，PB2，PQ2三者之间的数量关系为 PD2+PB2=PQ2PD2+PB2=PQ2；
（2）如图②，若点P在DB的延长线上，则（1）中所猜想的结论是否仍然成立？请利用图②给出证明过程．
AB
=
2
【答案】BO⊥DB；PD2+PB2=PQ2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/10 8:0:8组卷：72引用：2难度：0.5
相似题
-
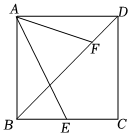1．如图，正方形ABCD的边长为4，点E是BC上的动点，点F在对角线BD上，若∠EAF=45°，BE=2，则AF的长为 ．发布：2025/6/9 17:0:1组卷：467引用：3难度：0.5 -
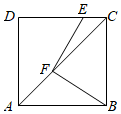2．如图，在边长为4的正方形ABCD中，点E，F分别在CD，AC上，BF⊥EF，CE=1，则AF的长是（ ）发布：2025/6/9 17:30:1组卷：3397引用：9难度：0.4 -
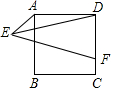3．如图，正方形ABCD的边长AB=8，E为平面内一动点，且AE=4，F为CD上一点，CF=2，连接EF，ED，则EF+ED的最小值为（ ）12发布：2025/6/9 18:30:1组卷：2521引用：5难度：0.3
