已知，如图（1），∠AOB和∠COD共顶点O，OB和OD重合，OM为∠AOD的平分线，ON为∠BOC的平分线，∠AOB=α，∠COD=β
（1）如图（2），若α=90°，β=30°，则，∠MON=60°60°
（2）若将∠COD绕O逆时针旋转至图（3）的位置，求∠MON（用α、β表示）
（3）如图（4），若α=2β，∠COD绕O逆时针旋转，转速为3°/秒，∠AOB绕O同时逆时针旋转，转速为1°/秒（转到OC与OA共线时停止运动），且OE平分∠BOD，请判断∠COE与∠AOD的数量关系并说明理由．
【答案】60°
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/12 15:0:1组卷：1175引用：4难度：0.1
相似题
-
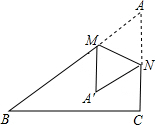1．如图，将三角形ABC纸片沿MN折叠，使点A落在点A′处，若∠A′MB=55°，则∠AMN=°．发布：2025/6/12 22:0:1组卷：316引用：6难度：0.7 -
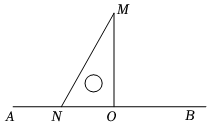2．如图，O为直线AB上一点，将一直角三角板（∠M=30°）的直角顶点放在点O处，一边ON在射线OA上，另一边OM在直线AB的上方．将三角板绕点O以每秒3°的速度沿逆时针方向旋转一周．则经过 秒后，MN⊥AB．发布：2025/6/12 10:30:1组卷：1543引用：7难度：0.5 -
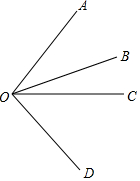3．已知：如图，∠AOB=30°，∠COB=20°，OC平分∠AOD．求∠COD的度数．
∵∠AOB=30°，∠COB=20°（已知），
∴∠AOC=∠+∠=°．
∵OC平分∠AOD，
∴∠AOC=∠（角平分线定义）．
∴∠COD=°．发布：2025/6/12 8:30:1组卷：485引用：3难度：0.9
