在平面直角坐标系中,坐标原点为点O,抛物线y=x2+bx+c(b,c为常数)的对称轴为直线x=1,且经过点A(-2,5).点P在该抛物线上,其横坐标为m.
(1)求此抛物线对应的函数表达式;
(2)当点P与点A关于抛物线的对称轴对称时,求△AOP的面积;
(3)以PA为对角线作矩形PBAC,矩形的四边均与坐标轴平行,当矩形与抛物线的另一个交点与矩形的某个顶点的连线将矩形面积分成1:3的两部分时,求m的值;
(4)设抛物线上点P与点A之间的部分(含端点)为图象G,当直线y=1-4m与图象G只有一个公共点时,直接写出m的取值范围.
【考点】二次函数综合题.
【答案】(1)y=x2-2x-3;
(2)△AOP的面积为15;
(3)m的值为2或10;
(4)或或m=.
(2)△AOP的面积为15;
(3)m的值为2或10;
(4)
m
≤
-
5
-
1
-
1
≤
m
<
5
-
1
5
4
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/10/23 1:0:2组卷:81引用:2难度:0.1
相似题
-
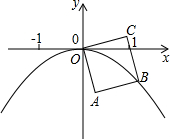 1.边长为1的正方形OA1B1C1的顶点A1在x轴的正半轴上,如图将正方形OA1B1C1绕顶点O顺时针旋转75°得正方形OABC,使点B恰好落在函数y=ax2(a<0)的图象上,则a的值为 .发布:2025/6/14 23:30:1组卷:2329引用:24难度:0.7
1.边长为1的正方形OA1B1C1的顶点A1在x轴的正半轴上,如图将正方形OA1B1C1绕顶点O顺时针旋转75°得正方形OABC,使点B恰好落在函数y=ax2(a<0)的图象上,则a的值为 .发布:2025/6/14 23:30:1组卷:2329引用:24难度:0.7 -
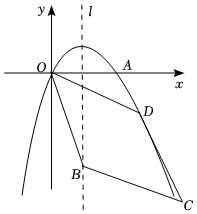 2.如图,在平面直角坐标系中,抛物线y=-x2+2x与x轴正半轴交于点A,点B在抛物线的对称轴上,点D在抛物线上,且在对称轴右侧,点C是平面内一点,四边形OBCD是平行四边形.
2.如图,在平面直角坐标系中,抛物线y=-x2+2x与x轴正半轴交于点A,点B在抛物线的对称轴上,点D在抛物线上,且在对称轴右侧,点C是平面内一点,四边形OBCD是平行四边形.
(1)求点A的坐标及抛物线的对称轴;
(2)若点B的纵坐标是-3,点D的横坐标是,则S▱OBCD=;52
(3)若点C在抛物线上,且▱OBCD的面积是12,请直接写出点C的坐标.发布:2025/6/14 21:0:1组卷:840引用:3难度:0.3 -
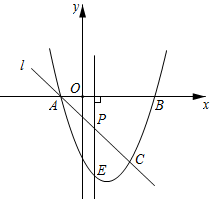 3.如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点,过点A的直线l交抛物线于点C(2,m).
3.如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点,过点A的直线l交抛物线于点C(2,m).
(1)求抛物线的解析式.
(2)点P是线段AC上一个动点,过点P作x轴的垂线交抛物线于点E,求线段PE最大时点P的坐标.
(3)点F是抛物线上的动点,在x轴上是否存在点D,使得以点A,C,D,F为顶点的四边形是平行四边形?如果存在,请直接写出所有满足条件的点D的坐标;如果不存在,请说明理由.发布:2025/6/14 23:30:1组卷:4755引用:21难度:0.1


