 阅读材料:
阅读材料:
①对于任意实数a和b,都有(a-b)2≥0,∴a2-2ab+b2≥0,于是得到a2+b2≥2ab,
当且仅当a=b时,等号成立.
②任意一个非负实数都可写成一个数的平方的形式.即:如果a≥0,则a=(a)2.
如:2=(2)2,3=(3)3等.
例:已知a>0,求证:a+12a≥2.
证明:∵a>0,∴a+12a=(a)2+(12a)2≥2×a×12a=2;
∴a+12a≥2,当且仅当a=22时,等号成立.
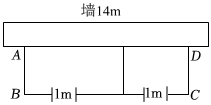
请阅读上述材料并解答下列问题:如图,某园艺公司准备围建一个矩形花圃,其中一边靠墙(墙的最大可用长度为14米),中间隔有一道篱笆的长方形花圃,为了方便出入,在建造篱笆花圃时,在BC上用其他材料做了宽为1米的两扇小门.
(1)若所用的篱笆长为22米.
①若花圃的面积刚好为45平方米,则此时花圃的AB段长为多少?
②这个花圃的面积最大面积能否达到50平方米?通过计算说明理由.
(2)若要围成面积为75平方米的花圃,需要用的篱笆最少是多少米?
a
=
(
a
)
2
2
=
(
2
)
2
,
3
=
(
3
)
3
a
+
1
2
a
≥
2
a
+
1
2
a
=
(
a
)
2
+
(
1
2
a
)
2
≥
2
×
a
×
1
2
a
=
2
a
+
1
2
a
≥
2
a
=
2
2
【考点】二次函数的应用;完全平方公式的几何背景.
【答案】(1)花圃的AB段长为5米;
(2)若要围成面积为75平方米的花圃,需要用的篱笆最少是28米.
(2)若要围成面积为75平方米的花圃,需要用的篱笆最少是28米.
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/5/23 8:0:8组卷:189引用:1难度:0.2
相似题
-
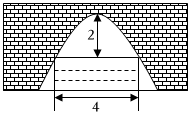 1.如图所示为一座纵截面为抛物线形状的拱桥,当水面宽4m时,拱顶(拱桥洞的最高点)离水面2m,当水位下降1m时,水面的宽度为( )发布:2025/6/8 9:0:1组卷:105引用:1难度:0.6
1.如图所示为一座纵截面为抛物线形状的拱桥,当水面宽4m时,拱顶(拱桥洞的最高点)离水面2m,当水位下降1m时,水面的宽度为( )发布:2025/6/8 9:0:1组卷:105引用:1难度:0.6 -
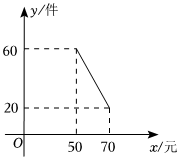 2.某商店试销一种新商品,新商品的进价为30元/件,经过一段时间的试销发现,每月的销售量会因售价的调整而不同.令每月销售量为y件,售价为x元/件,每月的总利润为Q元.
2.某商店试销一种新商品,新商品的进价为30元/件,经过一段时间的试销发现,每月的销售量会因售价的调整而不同.令每月销售量为y件,售价为x元/件,每月的总利润为Q元.
(1)当售价在40≤x≤50元时,每月销售量都为60件,则此时每月的总利润最多是多少元?
(2)当售价在50≤x≤70元时,每月销售量与售价的关系如图所示,则此时当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?发布:2025/6/8 9:0:1组卷:56引用:3难度:0.6 -
3.为了巩固脱贫攻坚成效,助推乡村振兴,最近市委市政府又出台了系列“惠农”政策,农民收入大幅增加.某村一农户生产经销一种农副产品,已知这种产品的成本为5元/千克,售价为6元/千克时,当天的销售量为100千克.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5千克.设当天销售单价统一为x元/千克(x≥6,且x是按0.5元的整数倍上涨),当天的销售利润为y元.
(1)求y与x之间的函数关系式,不要求写出自变量x的取值范围;
(2)若物价部门核定该产品的利润率不得超过80%,该产品的售价定为多少元时,才能使当天获得最大利润?最大利润是多少?发布:2025/6/8 8:0:6组卷:38引用:1难度:0.6


