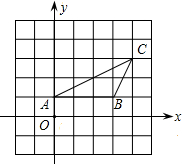
阅读：在平面直角坐标系中，已知两点的坐标，可构造直角三角形，运用勾股定理，求这两点间的距离；在平面直角坐标系中有两点A（-3，5），B（1，2），求A，B两点间的距离．过点A作x轴的垂线，过点B作y轴的垂线，相交于点C，连接AB．∴AC=|5-2|=3，BC=|1-（-3）|=4，在Rt△ABC中，由勾股定理得：

AB

=

A

C

2

+

B

C

2

=

3

2

+

4

2

=

5

，若M（x₁，y₁），N（x₂，y₂），从而得到两点间的距离公式

MN

=

（

x

1

-

x

2

）

2

+

（

y

1

-

y

2

）

2

．解决下列问题：

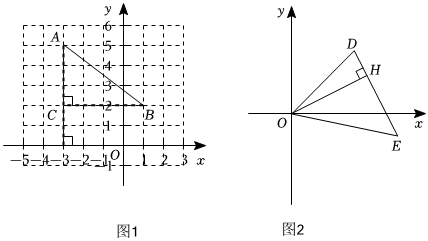
（1）若P（2，4），Q（-3，-8），则PQ两点间的距离PQ=

13

13

；
（2）如图2：点D（3，3），点E（5，-1），则DE=

2

5

2

5

，若OH⊥DE，则OH=

9

5

5

9

5

5

．