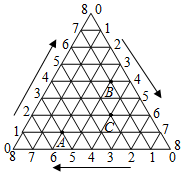
如图，将一等边三角形的三条边各8等分，按顺时针方向（图中箭头方向）标注各等分点的序号0、1、2、3、4、5、6、7、8，将不同边上的序号和为8的两点依次连接起来，这样就建立了“三角形”坐标系．在建立的“三角形”坐标系内，每一点的坐标用过这一点且平行（或重合）于原三角形三条边的直线与三边交点的序号来表示（水平方向开始、按顺时针方向、取与三角形外箭头方向一致的一侧序号），如点A的坐标可表示为（1，2，5），点B的坐标可表示为（4，3，1），按此方法，若点C的坐标为（2，m,m-2），则m=（ ）
【考点】等边三角形的性质；规律型：数字的变化类．
【答案】C
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/27 14:0:0组卷：71引用：1难度：0.6
相似题
-
1．等边△ABC的周长为12cm,则它的面积为cm2．
发布：2025/6/15 13:0:6组卷：339引用：20难度：0.7 -
2．已知，△ABC是等边三角形，将一块含有30°角的直角三角板DEF如图放置，让三角板在BC所在的直线上向右平移，如图1，当点E与点B重合时，点A恰好落在三角形的斜边DF上．
（1）利用图1证明：EF=2BC；
（2）在三角板的平移过程中，在图2中线段EB=AH是否始终成立（假定AB，AC与三角板斜边的交点为G、H）？如果成立，请证明；如果不成立，请说明理由．
发布：2025/6/15 12:30:1组卷：780引用：8难度：0.3 -
3．等边△ABC的两条角平分线BD和CE交于点I，则∠BIC等于（ ）
发布：2025/6/15 12:30:1组卷：445引用：12难度：0.7
